
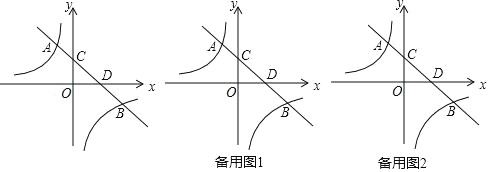
����Ŀ����ͼ��ֱ�� y=��x+2 �뷴�������� y=![]() ��k��0����ͼ���� A��a��3����B��3��b�����㣬ֱ�� AB �� y ���ڵ� C���� x ���ڵ� D��
��k��0����ͼ���� A��a��3����B��3��b�����㣬ֱ�� AB �� y ���ڵ� C���� x ���ڵ� D��
(1)��ֱ��д�� a=_______��b=______�������������Ľ���ʽΪ_______��
(2)�� x �����Ƿ����һ�� E��ʹ����EBD=��OAC��������������� E �����꣬ �������ڣ���˵�����ɣ�
(3)��P �� x ���ϵĶ��㣬�� Q ��ƽ���ڵĶ��㣬���� A��B��P��Q Ϊ������ı����Ǿ��Σ�������������� Q �����꣬����������˵�����ɣ�
���𰸡�(1)-1��-1��-3��(2)���������ĵ� E ����Ϊ��0��0����![]() ��0����(3)���������ĵ� Q ����Ϊ��0����4����0��4����1+
��0����(3)���������ĵ� Q ����Ϊ��0����4����0��4����1+![]() ��2����1��
��2����1��![]() ��2����
��2����
��������
��1�����ô���ϵ�������ɽ�����⣻
���������Σ��ٵ��� E �� O �غ�ʱ����EBD=��OAC����ʱ E��0��0�������� BE���OA�����E��BD=��OAC���ֱ���⼴�ɽ�����⣻
���������λ���ͼ�Σ��ֱ���⼴�ɽ�����⣻
(1)��A��a��3����B��3��b�������� y=��x+2 �ϣ�
��a=��1��b=��1��
��A����1��3������3����1����
��A����1��3���� y=![]() �ϣ�
�ϣ�
��k=��3��
�ʴ�Ϊ��1����1����3��
��ͼ 1 �У����� OB��
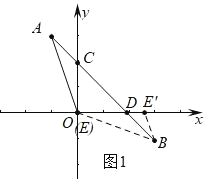
��A����1��3����B��3����1����
��OA=OB= ![]() ��
��
���OAC=��OBD��
������ E �� O �غ�ʱ����EBD=��OAC����ʱ E��0��0������ BE���OA������E��BD=��OAC��
������ D��2��0����
��AD= ![]() =3
=3![]() ��BD=
��BD= ![]() =
= ![]() ��
��
�� BE���OA��
��![]()
�� ![]() ��
��
��DE��=![]()
��OE��= ![]() ��
��
��E�䣨![]() ��0����
��0����
�������������������ĵ� E ����Ϊ��0��0����![]() ��0����
��0����
���ڣ���ͼ 2 �У�
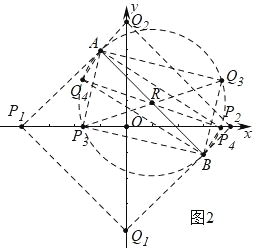
�����ı��� AP1Q1B �Ǿ���ʱ����֪ P1����4��0����
�� B��3����1������ƽ�� 3 ����λ������ƽ�� 3 ����λ�õ� Q1��0����4����
�����ı��� BP2Q2A �Ǿ���ʱ��P2��4��0����
�� A��3����1������ƽ��һ����λ������ƽ��һ����λ�õ� Q2��0��4����
���� AB �Ǿ��εĶԽ���ʱ���� AB ���е�Ϊ R��1��1������ P3��m��0����
��RP=2![]() ��
��
�ࣨ1��m��2+12=��2![]() ��2��
��2��
�� m=1+![]() �� 1��
�� 1��![]() ��
��
��P3��1��![]() ��0����P4��1+
��0����P4��1+![]() ��2����
��2����
��Q3��1+![]() ��2����Q4��1��
��2����Q4��1��![]() ��2����
��2����
�������������������ĵ� Q ����Ϊ��0����4����0��4����1+![]() ��2����1-
��2����1-![]() ��2����
��2����


 ̽���빮�̺��Ͽ�ѧ����������ϵ�д�
̽���빮�̺��Ͽ�ѧ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ֱ��������2��1����3����4�IJ�����Ƭ�����dz�����������ȫ����ͬ���ֽ����DZ��泯�ϣ�ϴ�Ⱥ�����ſ�Ƭ���������ȡһ�Ų��Żأ����ÿ�Ƭ�ϵ����ּ�Ϊm�����������ȡһ�ţ�����Ƭ�ϵ����ּ�Ϊn��
��1���뻭����״ͼ��д����m��n�����п��ܵĽ����
��2������ѡ����m��n��ʹһ�κ���y=mx+n��ͼ���ڶ������������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����Ƹһ��������Ա���Լס�����λӦ���߽��������Ժͱ��ԣ����ǵijɼ����ٷ��ƣ������ʾ��
Ӧ���� | ���� | ���� |
�� | 86 | 90 |
�� | 92 | 83 |
��1�������˾��Ϊ���Ժͱ���ͬ����Ҫ�������ǵijɼ�����˭����¼ȡ��
��2�������˾��Ϊ��Ϊ������Ա���Գɼ�Ӧ�ñȱ��Գɼ�����Ҫ�����ֱ�������6��4��Ȩ������ס������˸��Ե�ƽ���ɼ���˭����¼ȡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڽ�����AB�ϣ�����35 m������������AE������һ������CD�Ķ���D������������A��������Ϊ45������������E��������Ϊ37�㣮�����������ľ���BC��
(�����:sin37����0.6��cos37����0.8�� tan37����0.75)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
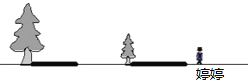
����Ŀ����������������С������һյ·���µ�Ӱ����ͼ��ʾ
��1��ȷ��·�Ƶ��ݵ�λ�ã��õ�P��ʾ���ͱ�ʾ���õ�Ӱ�����߶Σ����߶�AB��ʾ����
��2����С����Ϊ2m��Ӱ��Ϊ4m�����ø�1.5m��Ӱ��Ϊ4.5�ף������þ���С��10�ף������·�Ƶ��ݵĸ߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
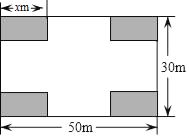
����Ŀ��ijС��ҵ��ίԱ�������һ�鳤50m����30m�ľ��οյؽ��ɽ����㳡����Ʒ�����ͼ��ʾ����Ӱ����Ϊ�̻������Ŀ��̻���Ϊȫ�ȵľ��Σ����հ�����Ϊ����������ܵ�4�����ڿ�����ͬ������Ȳ�С��14m��������26m�����̻����ϳ���Ϊxm����������Ϊym2
��1��ֱ��д��������x��ʽ�ӱ�ʾ���ڵĿ���Ϊ�� ����
��y��x�ĺ�����ϵʽ��x��ȡֵ��Χ�� ����
��2�����������y����������
��3��Ԥ�ƻ�����Ϊ50Ԫ/m2���̻������Ϊ40Ԫ/m2�����ҵ��ίԱ��Ͷ�ʲ��ó���72000Ԫ�����뽨�죬��xΪ����ʱ�����м��ֽ��췽����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ű߳�Ϊ40 cm��������Ӳֽ�壬�����ʵ��IJü����۳�һ�����������(ֽ��ĺ�Ⱥ��Բ���)��
(1)��ͼ������������Ӳֽ����ĽǸ�����һ��ͬ����С�������Σ���ʣ�ಿ���۳�һ���ǵij�������ӣ�

��Ҫʹ�۳ɵij�������ӵĵ����Ϊ484 cm2����ô�����������εı߳�Ϊ���٣�
���۳ɵij�������ӵIJ�����Ƿ������ֵ������У����������ֵ�ʹ�ʱ�����������εı߳������û�У�˵�����ɣ�
(2)����������Ӳֽ������ܼ���һЩ����(�������ľ���������һ������������Ӳֽ��ı���)����ʣ�ಿ���۳�һ���иǵij�������ӣ����۳ɵ�һ����������ӵı����Ϊ550 cm2�����ʱ��������ӵij���������(ֻ���������Ҫ���һ�����)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���A��C������ֱ�Ϊ��4��6������5��4������ABƽ����x�ᣬ������ABCD����ƽ�ƣ��õ�����A��B��C��D�䣮����A�䡢C��ͬʱ���ں���![]() ��ͼ���ϣ���k��ֵΪ��������
��ͼ���ϣ���k��ֵΪ��������
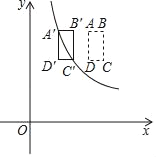
A. 6 B. 8 C. 10 D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ó�20�����Χ��һ��һ�濿ǽ�ij����εIJ�������Ŀ�Ϊx�ף����Ϊyƽ���ף�
��1����y��x�ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
��2������Χ����ʹ�����������������Ƕ��٣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com