
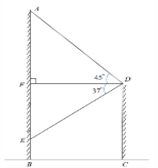
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

【答案】两建筑物间的距离BC为20m
【解析】试题分析:
如图,过点D作DF![]() AB交AB于点F,则∠DFA=∠DFE=90°,结合已知条件易得AF=DF,EF=DF·tan37°,结合AE=AF+EF=35即可列出方程解得DF的长,这样由四边形BCDF是矩形即可得到BC=DF从而求出BC的长了.
AB交AB于点F,则∠DFA=∠DFE=90°,结合已知条件易得AF=DF,EF=DF·tan37°,结合AE=AF+EF=35即可列出方程解得DF的长,这样由四边形BCDF是矩形即可得到BC=DF从而求出BC的长了.
试题解析:
过点D作DF![]() AB交AB于点F,
AB交AB于点F,
∴∠DFA=∠DFE=90°,
∵∠ABC=∠BCD=90°,
∴四边形BCDF是矩形,
∴BC=DF,
∵在Rt△ADF中,∠ADF=45°,
∴AF=DF,
∵在Rt△DFE中,∠EDF=37°,
∴EF=DF·tan37°,
又∵AF+EF=AE=35,
∴DF+DF·tan37°=35,
解得DF=BC=20(m)
答:两建筑物间的距离BC为20m.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
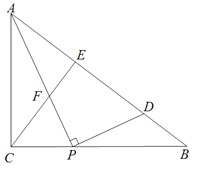
【题目】如图,已知△ABC中,∠ACB=90°,AC=15,BC=20.动点P在线段CB上,以1cm/s的速度从点C向B运动,连接AP,作CE⊥AB分别交AP、AB于点F、E,过点P作PD⊥AP交AB于点D.
(1)线段CE= ;
(2)若t=5时,求证:△BPD≌△ACF;
(3)t为何值时,△PDB是等腰三角形;
(4)求D点经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从A地出发去25km远的B地,甲骑车,乙步行,甲的速度是乙的速度的3倍,甲到达B地停留40min,然后从B地返回A地,在途中遇见乙,这时距他们出发的时间恰好为3h.
(1)若设乙的速度为x km/h,则甲的速度为 km/h,甲遇见乙时,乙走的路程可以表示为 km,甲走的路程可以表示为 km.
(2)两人的速度分别是多少?(请用方程来解决问题)
查看答案和解析>>
科目:初中数学 来源: 题型:
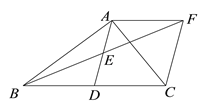
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
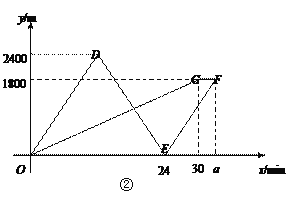
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.

(1)小明的速度为_________m/min,图②中a的值为__________.
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.
①写出小明妈妈在骑车由C处返回到A处的过程中,y与x的函数表达式及x的取值范围;
②在图③中画出整个过程中y与x的函数图像.(要求标出关键点的坐标)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]() -(+3.7)+(+
-(+3.7)+(+![]() )-(-1.7) (2)(-72)×2
)-(-1.7) (2)(-72)×2![]() ×(-
×(-![]() )÷(-3
)÷(-3![]() )
)
(3)(![]() -
-![]() -
-![]() +
+![]() )×(-24) (4)-32×(-2)+42÷(-2)3-∣-22∣
)×(-24) (4)-32×(-2)+42÷(-2)3-∣-22∣
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法,其中正确的个数是( )
①整数和分数统称为有理数;②绝对值是它本身的数只有0;③两数之和一定大于每个加数;④如果两个数积为0,那么至少有一个因数为0;⑤0是最小的有理数,;⑥数轴上表示互为相反数的点位于原点的两侧;⑦几个有理数相乘,如果负因数的个数是奇数,那么积为负数,
A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C,且OB=OC,下列结论:①b>1且b≠2;②b2﹣4ac<4a2;③a>![]() ;其中正确的个数为( )
;其中正确的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com