
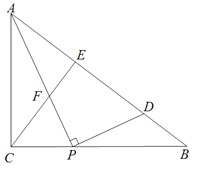
【题目】如图,已知△ABC中,∠ACB=90°,AC=15,BC=20.动点P在线段CB上,以1cm/s的速度从点C向B运动,连接AP,作CE⊥AB分别交AP、AB于点F、E,过点P作PD⊥AP交AB于点D.
(1)线段CE= ;
(2)若t=5时,求证:△BPD≌△ACF;
(3)t为何值时,△PDB是等腰三角形;
(4)求D点经过的路径长.
【答案】(1)12;(2)答案见解析;(3)![]() ;(4)12.5
;(4)12.5
【解析】试题分析:(1)由勾股定理求出AB的长,再由面积法即可得到结论;
(2)用ASA证明即可;
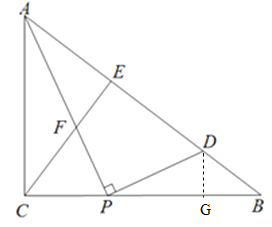
(3)作DG⊥BC,垂足为G,由(2)得∠CAP=∠GPD,可得△ACP∽△PGD.分三种情况讨论:①DP=DB,②PD=PB,③PB=DB;
(4)当AP平分∠CAB时,D′B最长,点CB上运动时,D在D′B之间往返运动.故点D运动路径的长=2BD′,求出BD′的长即可.
试题解析:解:(1)∵∠ACB=90°,AC=15,BC=20,∴AB=![]() =25.∵
=25.∵![]() ABCE=
ABCE=![]() ACBC,,∴25CE=15×20,解得:CE=12.
ACBC,,∴25CE=15×20,解得:CE=12.
(2)∵ t=5,∴BF=15,∴AC=BF
∵∠APC+∠BPD=∠APC+∠CAP=90° ,∴∠BPD=∠CAP.
∵∠ACE+∠BCE=∠BCE+∠B=90° ,∴∠ACE=∠B,∴△BPD≌△ACF.
(3)作DG⊥BC,垂足为G,由(2)得:∠CAP=∠GPD.∵∠ACP=∠PGD=90°,∴△ACP∽△PGD.分三种情况讨论:
①若DP=DB,则∠GPD=∠B ∴tan∠GPD=tan∠B=![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
②若PD=PB,则∠PDB=∠B.∵△ACP∽△PGD,∴∠APC=∠PDG.∵∠PDC>∠B,∴∠PDG>∠B=∠PDB,则点G在PB的延长线上,矛盾,故PD=PB不成立;
③若PB=DB,则BD=20-t.∵DG∥AC,∴DG:DB=AC:AB,GB:DB=CB:AB,∴DG:(20-t)=15:25,GB:(20-t)=20:25,解得:DG=![]() ,GB=
,GB=![]() ,∴PG=PB-GB=(20-t)-
,∴PG=PB-GB=(20-t)- ![]() =
=![]() .∵△ACP∽△PGD,∴AC:CP=PG:DG,∴15:t=
.∵△ACP∽△PGD,∴AC:CP=PG:DG,∴15:t=![]() ,解得:t=45>20,故PB=DB不成立.
,解得:t=45>20,故PB=DB不成立.
综上所述:t=![]() .
.
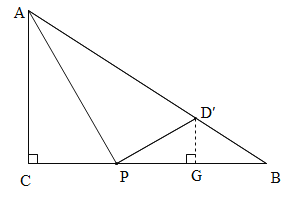
(4)方法一:当AP平分∠CAB时,D′B最长,点CB上运动时,D在D′B之间往返运动.故点D运动路径的长=2BD′.
∵AP平分∠CAB,∴AC:CP=AB:PB,∴15:CP=25:(20-CP),解得:CP=7.5.∵DG∥AC,∴![]() ,设DG=3x,则BG=4x,BD=5x.∵△D′PG∽△PAG,∴D′G:PG=CP:AC=1:2,∴PG=6x,∴6x+4x=PB=20-7.5,解得:x=1.25.∴2 BD′=2×1.25×5=12.5.
,设DG=3x,则BG=4x,BD=5x.∵△D′PG∽△PAG,∴D′G:PG=CP:AC=1:2,∴PG=6x,∴6x+4x=PB=20-7.5,解得:x=1.25.∴2 BD′=2×1.25×5=12.5.
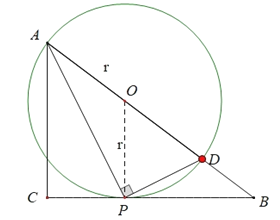
方法二:P点是在CB上运动的,而∠APD是直角,∴P可以看作是斜边AB上以AD为直径的圆O与线段CB的交点,当CB与⊙O相切的时候,此时的D是运动到最远的时候.设半径为OA=OP=r,则OB=25-r.∵OP∥AC,∴OP:AC=OB:AB,∴![]() ,r=
,r=![]() ,∴BD=25-
,∴BD=25-![]() =
=![]() ,∴运动路程为2BD=
,∴运动路程为2BD=![]() =12.5.
=12.5.


科目:初中数学 来源: 题型:
【题目】为了丰富学生的课外活动,某校决定购买100个篮球和a(a>10)副羽毛球拍.经调查发现:甲、乙两个体育用品商店以同样的价格出售同种品牌的篮球和羽毛球拍.已知每个篮球比每副羽毛球拍贵25元,两个篮球与三副羽毛球拍的费用正好相等.经洽谈,甲商店的优惠方案是:每购买十个篮球,送一副羽毛球拍;乙商店的优惠方案是:若购买篮球数超过80个,则购买羽毛球拍可打八折.
(1)设每个篮球x元,则每副羽毛球拍______元(用含x的代数表示);并求出每个篮球和每副羽毛球拍的价格分别是多少?
(2)请用含a的代数式分别表示出到甲商店和乙商店购买所花的费用;
(3)请你决策:在哪一家商店购买划算?(直接写出结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
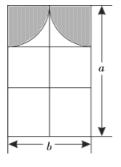
【题目】装修公司给小红家的窗户设计了如图所示的装修方案,上方布料窗眉(阴影部分)由两个半径相同的四分之一圆组成.
(1)分别用整式表示窗眉用布和窗户透光的面积.(窗框的面积忽略不计).
(2)观察(1)中的结果,它们是单项式还是多项式?次数分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
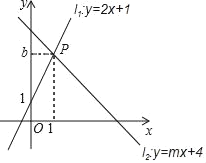
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值;
(2)垂直于x轴的直线与直线l1,l2,分别交于点C,D,垂足为点E,设点E的坐标为(a,0)若线段CD长为2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
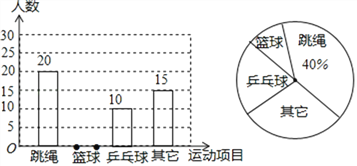
(1)在这次调查中,喜欢篮球项目的同学有多少人?
(2)在扇形统计图中,“乒乓球”的百分比为多少?
(3)如果学校有800名学生,估计全校学生中有多少人喜欢篮球项目?
(4)请将条形统计图补充完整.
(5)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请运用列表或树状图求出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
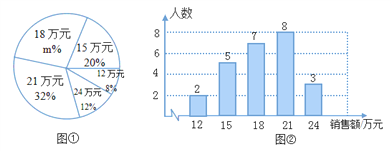
【题目】某商场服装部分为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组销售额的数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
该商场服装营业员的人数为 ,图①中m的值为 ;
求统计的这组销售额数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com