
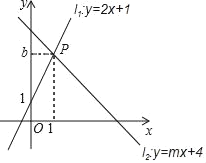
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
(1)求b,m的值;
(2)垂直于x轴的直线与直线l1,l2,分别交于点C,D,垂足为点E,设点E的坐标为(a,0)若线段CD长为2,求a的值.
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
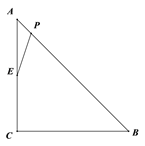
【题目】如图,Rt△ABC,∠C=90°,CA=CB=4![]() cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数
cm,点P为AB边上的一个动点,点E是CA边的中点, 连接PE,设A,P两点间的距离为xcm,P,E两点间的距离为y cm.小安根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小安的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y/cm | 2.8 | 2.2 | 2.0 | 2.2 | 2.8 | 3.6 | 5.4 | 6.3 |
(说明:补全表格时相关数值保留一位小数)
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①写出该函数的一条性质: ;
②当![]() 时,
时,![]() 的长度约为 cm.
的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:(![]() )﹣2﹣
)﹣2﹣![]() +(
+(![]() ﹣4)0﹣
﹣4)0﹣![]() cos45°.
cos45°.
【答案】1
【解析】试题分析:把原式的第一项根据负整数指数幂的意义化简,第二项根据算术平方根的定义求出9的算术平方根,第三项根据零指数公式化简,最后一项利用特殊角的三角函数值化简,合并后即可求出值.
试题解析:原式=4﹣3+1﹣![]()
=2﹣1
=1.
【题型】解答题
【结束】
16
【题目】《九章算术》“勾股”章有一题:“今有二人同所立,甲行率七,乙行率三.乙东行,甲南行十步而斜东北与乙会.问甲乙行各几何”.大意是说,已知甲、乙二人同时从同一地
点出发,甲的速度为7,乙的速度为3.乙一直向东走,甲先向南走10步,后又斜向北偏东方向走了一段后与乙相遇.那么相遇时,甲、乙各走了多远?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社推出一条成本价位500元/人的省内旅游线路,游客人数y(人/月)与旅游报价x(元/人)之间的关系为y=﹣x+1300,已知:旅游主管部门规定该旅游线路报价在800元/人~1200元/人之间.
(1)要将该旅游线路每月游客人数控制在200人以内,求该旅游线路报价的取值范围;
(2)求经营这条旅游线路每月所需要的最低成本;
(3)档这条旅游线路的旅游报价为多少时,可获得最大利润?最大利润是多少?
【答案】(1)取值范围为1100元/人~1200元/人之间;(2)50000;(3)x=900时,w最大=160000
【解析】试题分析:(1)根据题意列不等式求解可;
(2)根据报价减去成本可得到函数的解析式,根据一次函数的图像求解即可;
(3)根据利润等于人次乘以价格即可得到函数的解析式,然后根据二次函数的最值求解即可.
试题解析:(1)∵由题意得![]() 时,即
时,即![]() ,
,
∴解得![]()
即要将该旅游线路每月游客人数控制在200人以内,该旅游线路报价的取值范围为1100元/人~1200元/人之间;
(2)![]() ,
,![]() ,∴
,∴![]()
∵![]() ,∴当
,∴当![]() 时,z最低,即
时,z最低,即![]() ;
;
(3)利润![]()
当![]() 时,
时,![]() .
.
【题型】解答题
【结束】
23
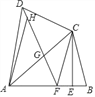
【题目】已知四边形ABCD中,AB=AD,对角线AC平分∠DAB,过点C作CE⊥AB于点E,点F为AB上一点,且EF=EB,连接DF.
(1)求证:CD=CF;
(2)连接DF,交AC于点G,求证:△DGC∽△ADC;
(3)若点H为线段DG上一点,连接AH,若∠ADC=2∠HAG,AD=3,DC=2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上两点间的距离等于这两点所对应的数的差的绝对值.例:如图所示,点A、B在数轴上分别对应的数为a、b,则A、B两点间的距离表示为|AB|=|a﹣b|.
![]()
根据以上知识解题:
(1)若数轴上两点A、B表示的数为x、﹣1,
①A、B之间的距离可用含x的式子表示为 ;
②若该两点之间的距离为2,那么x值为 .
(2)|x+1|+|x﹣2|的最小值为 ,此时x的取值是 ;
(3)已知(|x+1|+|x﹣2|)(|y﹣3|+|y+2|)=15,求x﹣2y的最大值 和最小值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
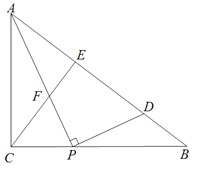
【题目】如图,已知△ABC中,∠ACB=90°,AC=15,BC=20.动点P在线段CB上,以1cm/s的速度从点C向B运动,连接AP,作CE⊥AB分别交AP、AB于点F、E,过点P作PD⊥AP交AB于点D.
(1)线段CE= ;
(2)若t=5时,求证:△BPD≌△ACF;
(3)t为何值时,△PDB是等腰三角形;
(4)求D点经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为24厘米.甲、乙两动点同时从顶点A出发,甲以2厘米/秒的速度沿正方形的边按顺时针方向移动,乙以4厘米/秒的速度沿正方形的边按逆时针方向移动,每次相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动,则第四次相遇时甲与最近顶点的距离是______厘米.

查看答案和解析>>
科目:初中数学 来源: 题型:
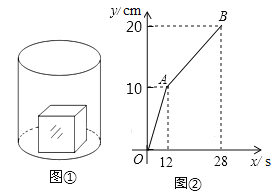
【题目】(2017·吉林)如图①,一个正方体铁块放置在圆柱形水槽内,现以一定的速度往水槽中注水,28s时注满水槽.水槽内水面的高度y(cm)与注水时间x(s)之间的函数图象如图②所示.
(1)正方体的棱长为 cm;
(2)求线段AB对应的函数解析式,并写出自变量x的取值范围;
(3)如果将正方体铁块取出,又经过t(s)恰好将此水槽注满,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
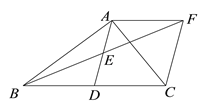
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF.
(1)求证:△AEF≌△DEB;
(2)若∠BAC=90°,求证:四边形ADCF是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com