
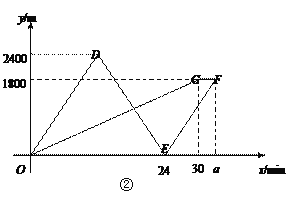
【题目】如图①,点A表示小明家,点B表示学校.小明妈妈骑车带着小明去学校,到达C处时发现数学书没带,于是妈妈立即骑车原路回家拿书后再追赶小明,同时小明步行去学校,到达学校后等待妈妈.假设拿书时间忽略不计,小明和妈妈在整个运动过程中分别保持匀速.妈妈从C处出发x分钟时离C处的距离为y1米,小明离C处的距离为y2米,如图②,折线O-D-E-F表示y1与x的函数图像;折线O-G-F表示y2与x的函数图像.

(1)小明的速度为_________m/min,图②中a的值为__________.
(2)设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米.
①写出小明妈妈在骑车由C处返回到A处的过程中,y与x的函数表达式及x的取值范围;
②在图③中画出整个过程中y与x的函数图像.(要求标出关键点的坐标)

【答案】 60 33
【解析】试题分析:
(1)由图可知,①C处距离学校1800米,小明从C处到学校用时30分钟,由此即可求得小明的速度为1800÷30=60(米/分钟);②C处距离小明家2400米,小明妈妈从C处到家再到C处用时24分钟,由此可得小明妈妈的速度为2400×2÷24=200(米/分钟),由此可得a=(2400×2+1800)÷200=33(分钟);
(2)①由(1)可知小明妈妈的速度为200米/分钟,小明的速度为60米/分钟可得y=260x(![]() );②由题意可知,y与x的函数关系分为三段:第一段
);②由题意可知,y与x的函数关系分为三段:第一段![]() ,第二段
,第二段![]() ,第三段
,第三段![]() ,结合题中已知条件可得当
,结合题中已知条件可得当![]() 时,y=0;当x=12时,y=3120;当x=30时,y=600;当x=33时,y=0;由此即可画出整个过程中y与x的函数图象了.
时,y=0;当x=12时,y=3120;当x=30时,y=600;当x=33时,y=0;由此即可画出整个过程中y与x的函数图象了.
试题解析:
(1)①由图1和图2中的信息可知:C处距离学校1800米,小明由C处到学校用了30分钟,
∴小明的速度=1800÷30=60(米/分钟);
②由图1和图2中的信息可知: C处距离小明家2400米,小明妈妈从C处到家再到C处用时24分钟,
∴小明妈妈的速度为2400×2÷24=200(米/分钟),
∵C处距离学校1800米,
∴a=(2400×2+1800)÷200=33(分钟);
(2)①由(1)可知小明妈妈的速度是:200 米/分钟,小明的速度是60米/分钟,
∵小明妈妈在骑车由C回到A的过程中,小明与妈妈背向而行,
∴y=260x, x的取值范围是0≤x≤12.
②由题意可得,整个过程中,y与x的函数图象如下图所示:
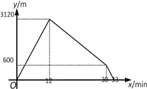 .
.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
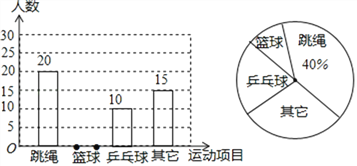
(1)在这次调查中,喜欢篮球项目的同学有多少人?
(2)在扇形统计图中,“乒乓球”的百分比为多少?
(3)如果学校有800名学生,估计全校学生中有多少人喜欢篮球项目?
(4)请将条形统计图补充完整.
(5)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请运用列表或树状图求出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作:将一把三角尺放在如图①的正方形![]() 中,使它的直角顶点
中,使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() ,探究:
,探究:
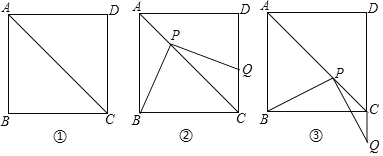
(1)如图②,当点![]() 在
在![]() 上时,求证:
上时,求证:![]() .
.
(2)如图③,当点![]() 在
在![]() 延长线上时,①中的结论还成立吗?简要说明理由.
延长线上时,①中的结论还成立吗?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=![]() ,线段AB的中点表示的数为
,线段AB的中点表示的数为![]() .
.
(问题情境)如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.
(综合运用)(1)点B表示的数是__________.
(2)若BC:AC=4:7,求点C到原点的距离.
(3)如图2,在(2)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(4)如图3,在(2)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒,1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问PT-MN的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
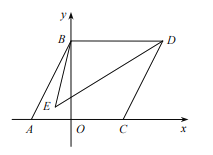
【题目】如图,在平面直角坐标系中,已知点![]() ,
,![]() ,将线段
,将线段![]() 沿着
沿着![]() 轴向右平移至
轴向右平移至![]() ,使点
,使点![]() 与点
与点![]() 对应,点
对应,点![]() 与点
与点![]() 对应,连接
对应,连接![]() .
.
(1)若![]() ,
,![]() 满足
满足![]() .
.
①填空:![]() _______,
_______,![]() _______;
_______;
②若面积关系![]() 成立,则点
成立,则点![]() 的坐标为_______;
的坐标为_______;
(2)![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,判断
,判断![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
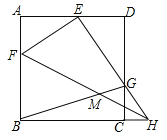
【题目】正方形ABCD中,F是AB上一点,H是BC延长线上一点,连接FH,将△FBH沿FH翻折,使点B的对应点E落在AD上,EH与CD交于点G,连接BG交FH于点M,当GB平分∠CGE时,BM=2![]() ,AE=8,则ED=______.
,AE=8,则ED=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与探究
宽与长的比是![]() (约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
(约0.618)的矩形叫做黄金矩形。黄金矩形给我们以协调、均匀的美感。世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计。
下面我们通过折纸得到黄金矩形。
第一步,在一张矩形纸片的一端,利用图1的方法折出一个正方形,然后把纸片展平。

第二步,如图2,把这个正方形折成两个相等的矩形,再把纸片展平,折痕是![]() 。
。
第三步,折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图3中所示的
折到图3中所示的![]() 处,折痕为
处,折痕为![]() 。
。
第四步,展平纸片,按照所得的点![]() 折出
折出![]() ,使
,使![]() ;过点
;过点![]() 折出折痕
折出折痕![]() ,使
,使![]() 。
。

(1)上述第三步将![]() 折到
折到![]() 处后,得到一个四边形
处后,得到一个四边形![]() ,请判断四边形
,请判断四边形![]() 的形状,并说明理由。
的形状,并说明理由。
(2)上述第四步折出折痕![]() 后得到一个四边形
后得到一个四边形![]() ,这个四边形是黄金矩形,请你说明理由。(提示:设
,这个四边形是黄金矩形,请你说明理由。(提示:设![]() 的长度为2)
的长度为2)
(3)在图4中,再找出一个黄金矩形_______________________________(黄金矩形![]() 除外,直接写出答案,不需证明,可能参考数值:
除外,直接写出答案,不需证明,可能参考数值:![]() )
)
(4)请你举一个采用了黄金矩形设计的世界名建筑_________________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com