
【题目】某公司欲招聘一名公务人员,对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示:
应试者 | 面试 | 笔试 |
甲 | 86 | 90 |
乙 | 92 | 83 |
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为作为公务人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
科目:初中数学 来源: 题型:
【题目】阅读材料:若关于x的一元二次方程![]() 的根均为整数,称该方程为“快乐方程”. 我们发现任何一个“快乐方程”的判别式
的根均为整数,称该方程为“快乐方程”. 我们发现任何一个“快乐方程”的判别式![]() 一定为完全平方数. 规定
一定为完全平方数. 规定![]() 为该“快乐方程”的“快乐数”. 若有另一个“快乐方程”
为该“快乐方程”的“快乐数”. 若有另一个“快乐方程”![]() 的“快乐数”为
的“快乐数”为![]() 且满足
且满足![]() ,则称
,则称![]() 互为“乐呵数”. 例如:“快乐方程”
互为“乐呵数”. 例如:“快乐方程”![]() 的两根均为整数,其判别式
的两根均为整数,其判别式![]() ,其“快乐数”
,其“快乐数”![]()
(1)“快乐方程”![]() 的“快乐数”为 ,若关于x的一元二次方程
的“快乐数”为 ,若关于x的一元二次方程![]() (m为整数,且5<m<22)是“快乐方程”,求其“快乐数”;
(m为整数,且5<m<22)是“快乐方程”,求其“快乐数”;
(2)若关于x的一元二次方程![]() 与
与![]() (m、n均为整数)都是“快乐方程”,且其“快乐数”互为“乐呵数”,求n的值.
(m、n均为整数)都是“快乐方程”,且其“快乐数”互为“乐呵数”,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
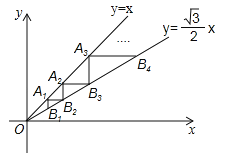
【题目】(2017辽宁省盘锦市,第18题,3分)如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线![]() 于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线
于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线![]() 于点B3,…,按照此规律进行下去,则点An的横坐标为______.
于点B3,…,按照此规律进行下去,则点An的横坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=k1x的图象与反比例函数![]() 的图象的一个交点是(1,3).
的图象的一个交点是(1,3).
(1)写出这两个函数的表达式,并确定这两个函数图象的另一个交点的坐标;
(2)画出草图,并据此写出使反比例函数大于正比例函数的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在平均每天获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
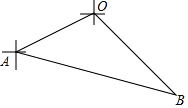
【题目】如图,甲、乙两渔船同时从港口O出发外出捕鱼,乙沿南偏东30°方向以每小时10海里的速度航行,甲沿南偏西75°方向以每小时10![]() 海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为________海里/小时?
海里的速度航行,当航行1小时后,甲在A处发现自己的渔具掉在乙船上,于是迅速改变航向和速度,仍以匀速沿南偏东60°方向追赶乙船,正好在B处追上.则甲船追赶乙船的速度为________海里/小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
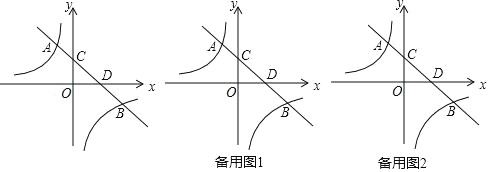
【题目】如图,直线 y=﹣x+2 与反比例函数 y=![]() (k≠0)的图象交于 A(a,3)、B(3,b)两点,直线 AB 交 y 轴于点 C、交 x 轴于点 D.
(k≠0)的图象交于 A(a,3)、B(3,b)两点,直线 AB 交 y 轴于点 C、交 x 轴于点 D.
(1)请直接写出 a=_______,b=______,反比例函数的解析式为_______.
(2)在 x 轴上是否存在一点 E,使得∠EBD=∠OAC,若存在请求出点 E 的坐标, 若不存在,请说明理由.
(3)点P 是 x 轴上的动点,点 Q 是平面内的动点,是以 A、B、P、Q 为顶点的四边形是矩形,若存在请求出点 Q 的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
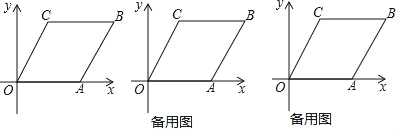
【题目】如图,在边长为5的菱形OABC中,sin∠AOC=![]() ,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:
,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:
(1)当CP⊥OA时,求t的值;
(2)当t<10时,求点P的坐标(结果用含t的代数式表示);
(3)以点P为圆心,以OP为半径画圆,当⊙P与菱形OABC的一边所在直线相切时,请直接写出t的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com