
【题目】已知正比例函数y=k1x的图象与反比例函数![]() 的图象的一个交点是(1,3).
的图象的一个交点是(1,3).
(1)写出这两个函数的表达式,并确定这两个函数图象的另一个交点的坐标;
(2)画出草图,并据此写出使反比例函数大于正比例函数的x的取值范围.
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共4只,某学习小组做摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.如表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1 000 |
摸到白球的次数m | 28 | 34 | 48 | 130 | 197 | 251 |
摸到白球的频率 | 0.28 | 0.23 | 0.24 | 0.26 | 0.246 | 0.251 |
(1)请估计:当n很大时,摸到白球的频率将会接近 (精确到0.01);
(2)试估算口袋中白种颜色的球有多少只?
(3)请根据估算的结果思考从口袋中先摸出一球,不放回,再摸出一球,这两只球颜色不同的概率是多少?画出树状图(或列表)表示所有可能的结果,并计算概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小丽准备测一根旗杆AB的高度,已知小丽的眼睛离地面的距离EC=1.5米,第一次测量点C和第二次测量点D之间的距离CD=10米,∠AEG=30°,∠AFG=60°,请你帮小丽计算出这根旗杆的高度.(结果保留根号)
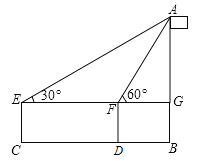
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人玩“锤子、石头、剪子、布”游戏.他们在不透明的袋子中放入形状、大小均相同的19张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为3、4、5、7,两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设θ为直角三角形的一个锐角,给出θ角三角函数的两条基本性质:①tanθ=![]() ;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ=
;②cos2θ+sin2θ=1,利用这些性质解答本题.已知cosθ+sinθ=![]() ,求值:
,求值:
(1)tanθ+![]() ; (2)|cosθ-sinθ|.
; (2)|cosθ-sinθ|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名公务人员,对甲、乙两位应试者进行了面试和笔试,他们的成绩(百分制)如表所示:
应试者 | 面试 | 笔试 |
甲 | 86 | 90 |
乙 | 92 | 83 |
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为作为公务人员面试成绩应该比笔试成绩更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,谁将被录取?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A、C的坐标分别为(4,6)、(5,4),且AB平行于x轴,将矩形ABCD向左平移,得到矩形A′B′C′D′.若点A′、C′同时落在函数![]() 的图象上,则k的值为( )
的图象上,则k的值为( )
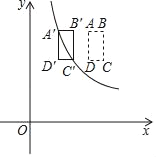
A. 6 B. 8 C. 10 D. 12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com