
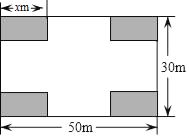
����Ŀ��ijС��ҵ��ίԱ�������һ�鳤50m����30m�ľ��οյؽ��ɽ����㳡����Ʒ�����ͼ��ʾ����Ӱ����Ϊ�̻������Ŀ��̻���Ϊȫ�ȵľ��Σ����հ�����Ϊ����������ܵ�4�����ڿ�����ͬ������Ȳ�С��14m��������26m�����̻����ϳ���Ϊxm����������Ϊym2
��1��ֱ��д��������x��ʽ�ӱ�ʾ���ڵĿ���Ϊ�� ����
��y��x�ĺ�����ϵʽ��x��ȡֵ��Χ�� ����
��2�����������y����������
��3��Ԥ�ƻ�����Ϊ50Ԫ/m2���̻������Ϊ40Ԫ/m2�����ҵ��ίԱ��Ͷ�ʲ��ó���72000Ԫ�����뽨�죬��xΪ����ʱ�����м��ֽ��췽����
���𰸡���1����50��2x����y����4x2+40x+1500��12��x��18������2��1404m2����3������4�ֽ��췽����
��������
��1���پ��εij���ȥ�����̻����ϳ��������.
��y=��������-4���̻������������![]() �ó�x�ķ�Χ.
�ó�x�ķ�Χ.
��2����y����4x2+40x+1500����Ϊ����ʽ��4��x��5��2+1600���������������ʼ������.
��3�������Ϊw���������w����40��x��5��2+76000���������������ʺ�x��ȡֵ��Χ��ϼ������.
�⣺��1���ٳ��ڵĿ���Ϊ��50��2x��
�ڸ�������ã�y��50��30��4x��x��10����
��y��x�ĺ�����ϵʽ��x��ȡֵ��ΧΪ��y����4x2+40x+1500��12��x��18����
�ʴ�Ϊ��50��2x��y����4x2+40x+1500��12��x��18����
��2��y����4x2+40x+1500����4��x��5��2+1600��
��a����4��0�������ߵĿ������£��Գ���Ϊx��5����12��x��18ʱ��y��x���������С��
�൱x��12ʱ��y�����1404��
�𣺻�������y��������Ϊ1404m2��
��3�������Ϊw��
������ã�w��50����4x2+40x+1500��+40��4x��x��10������40��x��5��2+76000��
�൱w��72000ʱ����ã�x1����5��x2��15��
��a����40��0��
�൱x����5��x��15ʱ��w��72000��
��12��x��18��
��15��x��18����x������
���4�ֽ��췽����


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O��������ABCD�Խ���BD���е㣮
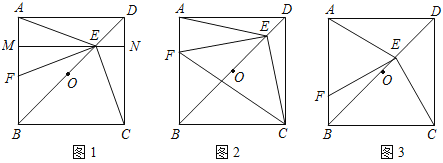
(1)��ͼ1������E��OD���е㣬��F��AB��һ�㣬��ʹ����CEF=90�㣬����E��ME��AD����AB�ڵ�M����CD�ڵ�N��
����AEM=��FEM�� ����F��AB���е㣻
(2)��ͼ2������E��OD��һ�㣬��F��AB��һ�㣬��ʹ![]() �����ж���EFC����״����˵�����ɣ�
�����ж���EFC����״����˵�����ɣ�
(3)��ͼ3����E��OD�ϵĶ���(����O��D�غ�)������CE����E����EF��CE����AB�ڵ�F����![]() ʱ�������
ʱ�������![]() ��ֵ(��ֱ��д������)��
��ֵ(��ֱ��д������)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ɽ���ز�ר�������ۺ��ң������Ϊÿǧ��40Ԫ����ÿǧ��60Ԫ���ۣ�ƽ��ÿ����۳�100ǧ�ˣ����������г����鷢�֣�����ÿ����2Ԫ����ƽ��ÿ������ۿ�����20ǧ�ˣ�����ר�����������ֺ���Ҫ��ƽ��ÿ�����2240Ԫ����ش�
��1��ÿǧ�˺���Ӧ���۶���Ԫ��
��2����ƽ��ÿ��������������£�Ϊ�����������ڹ˿ͣ�Ӯ���г����õ�Ӧ��ԭ�ۼ۵ļ��۳��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
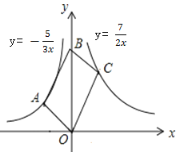
����Ŀ����ͼ��ƽ���ı���OABC�Ķ���O��B��y���ϣ�����A�ڷ���������y=![]() �ϣ�����C�ڷ���������y=
�ϣ�����C�ڷ���������y=![]() �ϣ���ƽ���ı���OABC�������____________��
�ϣ���ƽ���ı���OABC�������____________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
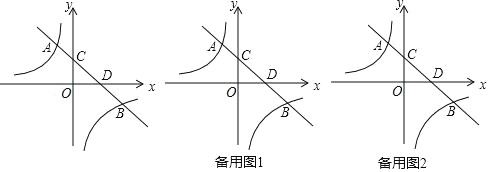
����Ŀ����ͼ��ֱ�� y=��x+2 �뷴�������� y=![]() ��k��0����ͼ���� A��a��3����B��3��b�����㣬ֱ�� AB �� y ���ڵ� C���� x ���ڵ� D��
��k��0����ͼ���� A��a��3����B��3��b�����㣬ֱ�� AB �� y ���ڵ� C���� x ���ڵ� D��
(1)��ֱ��д�� a=_______��b=______�������������Ľ���ʽΪ_______��
(2)�� x �����Ƿ����һ�� E��ʹ����EBD=��OAC��������������� E �����꣬ �������ڣ���˵�����ɣ�
(3)��P �� x ���ϵĶ��㣬�� Q ��ƽ���ڵĶ��㣬���� A��B��P��Q Ϊ������ı����Ǿ��Σ�������������� Q �����꣬����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
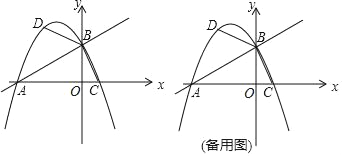
����Ŀ����ͼ��ֱ��y��![]() x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��������y����
x+2��x�ύ�ڵ�A����y�ύ�ڵ�B��������y����![]() x2+bx+c����A��B���㣬��x�����һ������Ϊ C��
x2+bx+c����A��B���㣬��x�����һ������Ϊ C��
��1���������ߵĽ���ʽ��
��2��ֱ��AB�Ϸ��������ϵĵ�D��ʹ�á�DBA��2��BAC����D������ꣻ
��3��M��ƽ����һ�㣬����BOC�Ƶ�M��ʱ����ת90���õ���B1O1C1������B1O1C1����������ǡ�������������ϣ������B1�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
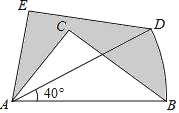
����Ŀ����ͼ������ABC�У�AB��5��AC��3��BC��4������ABC��A��ʱ�뷽����ת40���õ���ADE����B������·��Ϊ��BD����ͼ����Ӱ���֣���ABC����IJ��֣������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
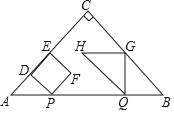
����Ŀ����ABC�ǵ���ֱ�������Σ���ACB��90�㣬AB��8cm������P��Q��2cm/s���ٶȷֱ�ӵ�A��Bͬʱ��������P��A��B���յ�B�˶�����Q��B��A���յ�A�˶�������P��PD��AC�ڵ�D����PDΪ�����Ҳ���������PDEF������Q��QG��AB��������BC��CA�ڵ�G���C���غϣ���QGΪ��������ֱ�ǡ�QGH���ҵ�GΪֱ�Ƕ��㣬��C��Hʼ����QG��ͬ�࣬��������PDEF���QGH�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����0��t��4����
��1������F�ڱ�QH��ʱ����t��ֵ��
��2����������PDEF���QGH�ص�����ͼ�����ı���ʱ����S��t֮��ĺ�����ϵʽ��
��3����FH���ڵ�ֱ��ƽ�л�ֱABʱ��ֱ��д��t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
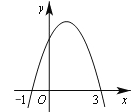
����Ŀ�����κ���y��ax2��bx��c��ͼ����ͼ��ʾ���������ж��д������
A��ͼ��ĶԳ�����ֱ��x��1 B����x��1ʱ��y��x���������С
C��һԪ���η���ax2��bx��c��0���������ǣ�1��3 D������1��x��3ʱ��y��0
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com