
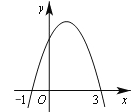
【题目】二次函数y=ax2+bx+c的图象如图所示,则下列判断中错误的是
A.图象的对称轴是直线x=1 B.当x>1时,y随x的增大而减小
C.一元二次方程ax2+bx+c=0的两个根是-1,3 D.当-1<x<3时,y<0
科目:初中数学 来源: 题型:
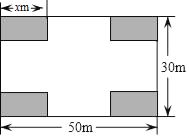
【题目】某小区业主委员会决定把一块长50m,宽30m的矩形空地建成健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14m,不大于26m,设绿化区较长边为xm,活动区的面积为ym2
(1)直接写出:①用x的式子表示出口的宽度为 ;
②y与x的函数关系式及x的取值范围 ;
(2)求活动区的面积y的最大面积;
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,如果业主委员会投资不得超过72000元来参与建造,当x为整数时,共有几种建造方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE、BF相交于H,BF、AD的延长线交于P.下面结论:
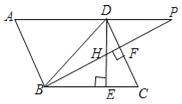
①![]() ,②∠A=∠BHE,③AB=BH,④△BHD∽△BDP.
,②∠A=∠BHE,③AB=BH,④△BHD∽△BDP.
请你把你认为正确的结论的番号都填上 (填错一个该题得0分)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为坐标原点,抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且O,C两点间的距离为3,x1x2<0,|x1|+|x2|=4,点A,C在直线y2=﹣3x+t上.
(1)当y1随着x的增大而增大时,求自变量x的取值范围;
(2)将抛物线y1向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n2﹣5n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用长20米的篱笆围成一个一面靠墙的长方形的菜园,设菜园的宽为x米,面积为y平方米.
(1)求y与x的函数关系式及自变量的取值范围;
(2)怎样围才能使菜园的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+bx+c(其中b,c为常数,c>0)的顶点恰为函数y=2x和y=![]() 的其中一个交点.则当a2+ab+c>2a>
的其中一个交点.则当a2+ab+c>2a>![]() 时,a的取值范围是
时,a的取值范围是
查看答案和解析>>
科目:初中数学 来源: 题型:
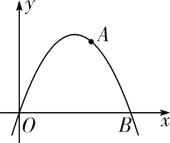
【题目】已知二次函数的解析式为y=-x2+4x,该二次函数交x轴于O、B两点,A为抛物线上一点,且横纵坐标相等(原点除外),P为二次函数上一动点,过P作x轴垂线,垂足为D(a,0)(a>0),并与直线OA交于点C.
(1)求A、B两点的坐标;
(2)当点P在线段OA上方时,过P作x轴的平行线与线段OA相交于点E,求△PCE周长的最大值及此时P点的坐标;
(3)当PC=CO时,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,关于![]() 的分式方程
的分式方程![]() .
.
(1)当![]() ,
,![]() 时,求分式方程的解;
时,求分式方程的解;
(2)当![]() 时,求
时,求![]() 为何值时分式方程
为何值时分式方程![]() 无解:
无解:
(3)若![]() ,且
,且![]() 、
、![]() 为正整数,当分式方程
为正整数,当分式方程![]() 的解为整数时,求
的解为整数时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在Rt△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,且CD=3cm,现有两个动点P,Q分别从点A和点B同时出发,其中点P以1cm/s的速度沿AC向终点C运动;点Q以1.25cm/s的速度沿BC向终点C运动,两点到达终点后停止运动。过点P作PE∥BC交AD于点E,连结EQ,设动点运动的时间为ts(t>0)。
(1) 连结DP,经过1s后,四边形EQDP能够成为平行四边形吗? 请说明理由;
(2) 当t为何值时,△EDQ为直角三角形?
(3) 如图②,设点M是EQ的中点,在点P、Q的整个运动过程中,试探究点M的运动路径长度是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com