
【题目】已知二次函数y=x2+bx+c(其中b,c为常数,c>0)的顶点恰为函数y=2x和y=![]() 的其中一个交点.则当a2+ab+c>2a>
的其中一个交点.则当a2+ab+c>2a>![]() 时,a的取值范围是
时,a的取值范围是
科目:初中数学 来源: 题型:
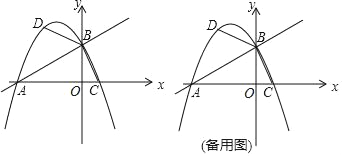
【题目】如图,直线y=![]() x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣
x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
(1)求抛物线的解析式;
(2)直线AB上方抛物线上的点D,使得∠DBA=2∠BAC,求D点的坐标;
(3)M是平面内一点,将△BOC绕点M逆时针旋转90°后,得到△B1O1C1,若△B1O1C1的两个顶点恰好落在抛物线上,请求点B1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
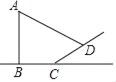
【题目】如图所示,小明准备测量学校旗杆AB的高度,他发现阳光下,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成锐角为26°,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度(精确到1m).(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售一款进价为每件40元的护肤品,调查发现,销售单价不低于40元且不高于80元时,该商品的日销售量y(件)与销售单价x(元)之间存在一次函数关系,当销售单价为44元时,日销售量为72件;当销售单价为48元时,日销售量为64件.
(1)求y与x之间的函数关系式;
(2)设该护肤品的日销售利润为w(元),当销售单价x为多少时,日销售利润w最大,最大日销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
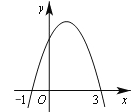
【题目】二次函数y=ax2+bx+c的图象如图所示,则下列判断中错误的是
A.图象的对称轴是直线x=1 B.当x>1时,y随x的增大而减小
C.一元二次方程ax2+bx+c=0的两个根是-1,3 D.当-1<x<3时,y<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种产品的进价为每件40元,现在的售价为每件60元,每星期可卖出300件.市场调查发现,该产品每降价1元,每星期可多卖出20件,由于供货方的原因销量不得超过380件,设这种产品每件降价x元(x为整数),每星期的销售利润为w元.
(1)求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)该产品销售价定为每件多少元时,每星期的销售利润最大?最大利润是多少元?
(3)该产品销售价在什么范围时,每星期的销售利润不低于6000元,请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
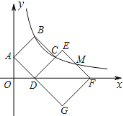
【题目】如图,正方形![]() 和正方形
和正方形![]() 的顶点
的顶点![]() 在
在![]() 轴上,顶点
轴上,顶点![]() ,
,![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 边上,反比例函数
边上,反比例函数![]() 的图象经过点
的图象经过点![]() 、
、![]() 和边
和边![]() 的中点
的中点![]() .若
.若![]() ,则正方形
,则正方形![]() 的面积为( )
的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
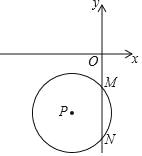
【题目】如图,半径为5的⊙P与y轴交于点M(0,﹣4),N(0,﹣10)
(1)求点P的坐标;
(2)将⊙P绕点O顺时针方向旋转90°后得⊙A,交x轴于B、C,求过A、B、C三个点的抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com