
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

【答案】2![]() +2
+2
【解析】如图所示,
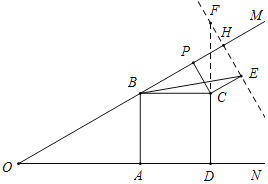
将BC绕着点C顺时针旋转90°得FC,作直线FE交OM于H,则∠BCF=90°,BC=FC,
∵将CP绕点C按顺时针方向旋转90°得CE,
∴∠PCE=90°,PC=EC,
∴∠BCP=∠FCE,
在△BCP和△FCE中,
BC=FC,∠BCP=∠FCE,PC=EC,
∴△BCP≌△FCE(SAS),
∴∠CBP=∠CFE,
又∵∠BCF=90°,
∴∠BHF=90°,
∴点E在直线FH上,即点E的轨迹为直线FH,
∵BH⊥EF,
∴当点E与点H重合时,BE=BH最短,
∵当CP⊥OM时,Rt△BCP中,∠CBP=30°,
∴CP=![]() BC=2,BP=
BC=2,BP=![]() CP=2
CP=2![]() ,
,
又∵∠PCE=∠CPH=∠PHE=90°,CP=CE,
∴正方形CPHE中,PH=CP=2,
∴BH=BH+PH=2![]() +2,
+2,
即BE的最小值为2![]() +2,
+2,
故答案为:2![]() +2.
+2.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】(本题满分10分)阅读下列材料:
(1)关于x的方程x2-3x+1=0(x≠0)方程两边同时乘以![]() 得:
得: ![]() 即
即![]() ,
, ![]() ,
,
(2)a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).
根据以上材料,解答下列问题:
(1)x2-4x+1=0(x≠0),则![]() = ______ ,
= ______ , ![]() = ______ ,
= ______ , ![]() = ______ ;
= ______ ;
(2)2x2-7x+2=0(x≠0),求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:某学校七年级8个班进行足球友谊赛,采用胜一场得3分,平一场得1分,负一场得0分的记分制.某班与其他7个队各赛1场后,以不败战绩积17分,那么该班共胜了几场比赛?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为选派一名学生参加全市实践活动技能竞赛,A,B两位同学在校实习基地现场进行加工直径为20mm的零件的测试,他俩加工的10个零件的相关数据依次如下图表所示(单位:mm).
根据测试得到的有关数据,试解答下列问题:
平均数 | 方差 | 完全符合要求的个数 | |
A | 20 | 0.026 | 2 |
B | 20 | S2B | 5 |
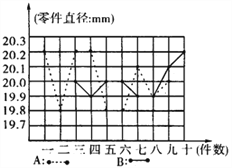
(1)考虑平均数与完全符合要求的个数,你认为________的成绩好些.
(2)计算出S2B的大小,考虑平均数与方差,说明谁的成绩好些.
(3)考虑图中折线走势及竞赛中加工零件个数远远超过10个的实际情况,你认为派谁去参赛较合适?说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com