
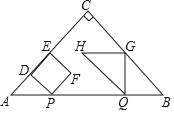
����Ŀ����ABC�ǵ���ֱ�������Σ���ACB��90�㣬AB��8cm������P��Q��2cm/s���ٶȷֱ�ӵ�A��Bͬʱ��������P��A��B���յ�B�˶�����Q��B��A���յ�A�˶�������P��PD��AC�ڵ�D����PDΪ�����Ҳ���������PDEF������Q��QG��AB��������BC��CA�ڵ�G���C���غϣ���QGΪ��������ֱ�ǡ�QGH���ҵ�GΪֱ�Ƕ��㣬��C��Hʼ����QG��ͬ�࣬��������PDEF���QGH�ص�����ͼ�ε����ΪS��cm2������P�˶���ʱ��Ϊt��s����0��t��4����
��1������F�ڱ�QH��ʱ����t��ֵ��
��2����������PDEF���QGH�ص�����ͼ�����ı���ʱ����S��t֮��ĺ�����ϵʽ��
��3����FH���ڵ�ֱ��ƽ�л�ֱABʱ��ֱ��д��t��ֵ��
���𰸡���1��t��![]() s;��2��������;��3��t��
s;��2��������;��3��t��![]() s��
s��![]() s��
s��![]() s��
s��
��������
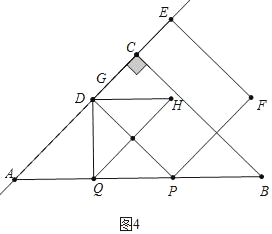
��1����ͼ1�У�����F�ڱ�QH��ʱ����֪AP��PQ��BQ�����AB�ij����ɽ�����⣻
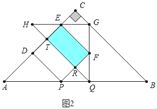
��2��������������ͼ2�У�����F��GQ��ʱ����֪AP��BQ��2t��PD��PF��![]() t��PQ��QF��t���г����̼��ɽ�����⣻����ͼ3�У��ص��������ı���GHRTʱ��
t��PQ��QF��t���г����̼��ɽ�����⣻����ͼ3�У��ص��������ı���GHRTʱ��
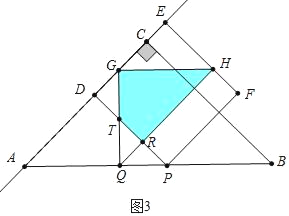
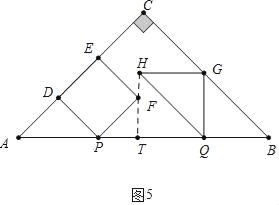
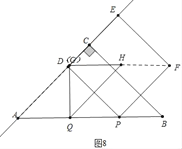
��3��������������������ͼ5�У���FH��ABʱ���ӳ�HF��AB��T����֪AP��BQ��GQ��HG��TQ��2t��PT��t������ͼ7�У���FH��ABʱ���ֱ��г����̼��ɽ�����⣮����ͼ8�У���HF��ABʱ��
�⣺��1����ͼ1�У�����F�ڱ�QH��ʱ����֪AP��PQ��BQ��
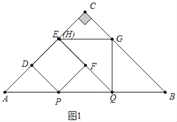
��Rt��ABC��AB��8��
��t![]() sʱ����F�ڱ�QH�ϣ�
sʱ����F�ڱ�QH�ϣ�
��2����ͼ2�У�����F��GQ��ʱ����֪AP=BQ=2t��PD=PF=![]() t��PQ=PF=t��
t��PQ=PF=t��
��2t+t+2t��8��
��t![]() ��
��
�ɣ�1����֪����![]() ʱ��������PDEF����QGH�ص�����ͼ�����ı���
ʱ��������PDEF����QGH�ص�����ͼ�����ı���
��ʱ![]()
��ͼ3�У���H��EF��ʱ������![]()
���t![]() ��
��
��ͼ4�У���G��D�غ�ʱ����֪4t��8��t�����t![]() ��
��
��![]() ʱ��
ʱ��![]()
��3������ͼ5�У���FH��ABʱ���ӳ�HF��AB��T����֪AP��BQ��GQ��HG��TQ��2t��PT��t��
��6t+t��8��
��t=![]() ��
��
����ͼ7�У���HF��AB��Tʱ��
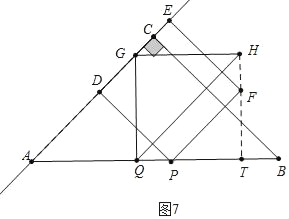
��TB��8��2��8��2t����8��3t�����t=![]() ��
��
����ͼ8�У���HF��ABʱ����t+2t��8��
��t=![]() ��
��
����������t=![]() s��
s��![]() s��
s��![]() sʱ��FH���ڵ�ֱ��ƽ�л�ֱ��AB��
sʱ��FH���ڵ�ֱ��ƽ�л�ֱ��AB��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������Ϊֱ�������ε�һ����ǣ������������Ǻ����������������ʣ���tan�ȣ�![]() ����cos2��+sin2�ȣ�1��������Щ���ʽ���⣮��֪cos��+sin�ȣ�
����cos2��+sin2�ȣ�1��������Щ���ʽ���⣮��֪cos��+sin�ȣ�![]() ����ֵ��
����ֵ��
(1)tan��+![]() �� (2)|cos��-sin��|��
�� (2)|cos��-sin��|��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
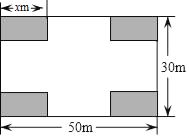
����Ŀ��ijС��ҵ��ίԱ�������һ�鳤50m����30m�ľ��οյؽ��ɽ����㳡����Ʒ�����ͼ��ʾ����Ӱ����Ϊ�̻������Ŀ��̻���Ϊȫ�ȵľ��Σ����հ�����Ϊ����������ܵ�4�����ڿ�����ͬ������Ȳ�С��14m��������26m�����̻����ϳ���Ϊxm����������Ϊym2
��1��ֱ��д��������x��ʽ�ӱ�ʾ���ڵĿ���Ϊ�� ����
��y��x�ĺ�����ϵʽ��x��ȡֵ��Χ�� ����
��2�����������y����������
��3��Ԥ�ƻ�����Ϊ50Ԫ/m2���̻������Ϊ40Ԫ/m2�����ҵ��ίԱ��Ͷ�ʲ��ó���72000Ԫ�����뽨�죬��xΪ����ʱ�����м��ֽ��췽����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��![]() �ֱ�����������A��B���㣬ֱ��y����2x��2�ֱ�����������C��D����
�ֱ�����������A��B���㣬ֱ��y����2x��2�ֱ�����������C��D����
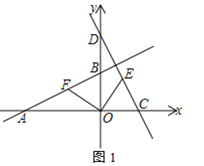
��1����A��B��C��D�ĵ������
��2����ͼ1����EΪֱ��CD��һ���㣬OF��OE��ֱ��AB�ڵ�F����֤��OE��OF
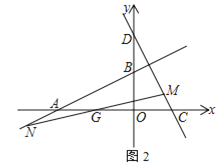
��3����ͼ2��ֱ��y��kx��k��x���ڵ�G���ֱ�ֱ��AB��CD��N��M���㣮��GM��GN����k��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABCD�Ķ���A��C������ֱ�Ϊ��4��6������5��4������ABƽ����x�ᣬ������ABCD����ƽ�ƣ��õ�����A��B��C��D�䣮����A�䡢C��ͬʱ���ں���![]() ��ͼ���ϣ���k��ֵΪ��������
��ͼ���ϣ���k��ֵΪ��������
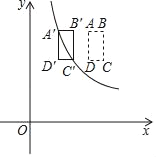
A. 6 B. 8 C. 10 D. 12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AD�ǡ�ABC����ǡ�EAC��ƽ���ߣ����ABC�����Բ���ڵ�D��AC��BD�ཻ�ڵ�F��
��1����֤��DB��DC��
��2����DA��DF����֤����BCF�ס�BDC��
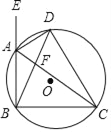
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У���DBC=45�㣬DE��BC��E��BF��CD��F��DE��BF�ཻ��H��BF��AD���ӳ��߽���P��������ۣ�
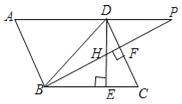
��![]() ���ڡ�A=��BHE����AB=BH���ܡ�BHD�ס�BDP��
���ڡ�A=��BHE����AB=BH���ܡ�BHD�ס�BDP��
���������Ϊ��ȷ�Ľ��۵ķ��Ŷ����� �����һ�������0�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OΪ����ԭ�㣬������y1=ax2+bx+c��a��0����x���ཻ�ڵ�A��x1��0����B��x2��0������y�ύ�ڵ�C����O��C�����ľ���Ϊ3��x1x2��0��|x1|+|x2|=4����A��C��ֱ��y2=��3x+t�ϣ�
��1����y1����x�����������ʱ�����Ա���x��ȡֵ��Χ��
��2����������y1����ƽ��n��n��0������λ����ƽ�ƺ�y����x�����������IJ���ΪP��ֱ��y2����ƽ��n����λ����ƽ�ƺ��ֱ����P�й�����ʱ����2n2��5n����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �ķ�ʽ����
�ķ�ʽ����![]() .
.
��1����![]() ��
��![]() ʱ�����ʽ���̵Ľ⣻
ʱ�����ʽ���̵Ľ⣻
��2����![]() ʱ����
ʱ����![]() Ϊ��ֵʱ��ʽ����
Ϊ��ֵʱ��ʽ����![]() �⣺
�⣺
��3����![]() ����
����![]() ��
��![]() Ϊ������������ʽ����
Ϊ������������ʽ����![]() �Ľ�Ϊ����ʱ����
�Ľ�Ϊ����ʱ����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com