
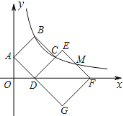
【题目】如图,在平面直角坐标系中,直线![]() 分别交两坐标轴于A、B两点,直线y=-2x+2分别交两坐标轴于C、D两点
分别交两坐标轴于A、B两点,直线y=-2x+2分别交两坐标轴于C、D两点
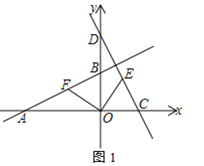
(1)求A、B、C、D四点的坐标
(2)如图1,点E为直线CD上一动点,OF⊥OE交直线AB于点F,求证:OE=OF
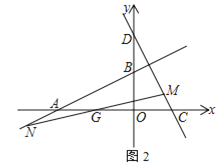
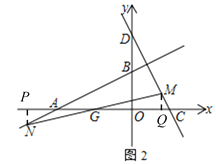
(3)如图2,直线y=kx+k交x轴于点G,分别交直线AB、CD于N、M两点.若GM=GN,求k的值
【答案】(1)![]() ,
,![]() ,
,![]() ,
,![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
(1)分别针对于直线AB. CD的解析式,令x=0和y=0, 解方程即可得出结论;
(2)先判断出AO=OD,OB=OC,得出△AOB≌△DOC (SAS) 。进而得出∠OAB=∠ODC,再利用同角的余角相等判断出∠AOF=∠BOE,得出△AOF≌△DOE (ASA),即可得出结论;
(3)先求出点G的坐标,设出点M、N的坐标,利用中点坐标公式建立方程组求解得出m,n,进而得出点M坐标,代入直线y=kx+k中,即可得出结论.
解:(1)∵![]()
∴令x=0,则y=1.
∴B(0,1)
∵![]()
令y=0, 则![]() ,
,
∴x=-2,
∴A(-2, 0)
∵![]()
令x=0,则y=2,
∴D(0,2),
∵![]()
令y=0,则-2x+2=0,
∴x=1 ,
∴C(1.0)
(2)由(1)知,A(-2,0),B(0,1),C(1,0),D(0,2),
∴OA=2,OB=1,OC=1,OD=2
∴![]() ,
,![]()
又∵∠AOB=∠DOC
∴![]()
∴∠OAB=∠ODC
∵![]()
∴∠BOF+∠BOE=90°
∵∠BOF+∠AOF=90°
∴![]()
∴![]()
∴![]()
(3)∵![]()
∴必过![]() 轴上一定点
轴上一定点![]()
分别作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]()
∵![]() ,
,
∴![]()
∴![]() ,
,![]()
设![]()
∴![]()
∴![]()
∴![]() 即
即![]() ,
,![]()
∴![]() 的解析式为
的解析式为![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里有 ![]() 个除颜色外都相同的球,其中有
个除颜色外都相同的球,其中有 ![]() 个红球,
个红球, ![]() 个黄球.
个黄球.
(1) 若从中随意摸出一个球,求摸出红球的可能性;
(2) 若要使从中随意摸出一个球是红球的可能性为 ![]() ,求袋子中需再加入几个红球?
,求袋子中需再加入几个红球?
查看答案和解析>>
科目:初中数学 来源: 题型:
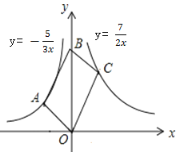
【题目】如图,平行四边形OABC的顶点O,B在y轴上,顶点A在反比例函数y=![]() 上,顶点C在反比例函数y=
上,顶点C在反比例函数y=![]() 上,则平行四边形OABC的面积是____________.
上,则平行四边形OABC的面积是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
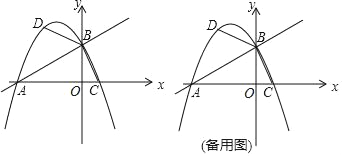
【题目】如图,直线y=![]() x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣
x+2与x轴交于点A,与y轴交于点B,抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
x2+bx+c经过A、B两点,与x轴的另一个交点为 C.
(1)求抛物线的解析式;
(2)直线AB上方抛物线上的点D,使得∠DBA=2∠BAC,求D点的坐标;
(3)M是平面内一点,将△BOC绕点M逆时针旋转90°后,得到△B1O1C1,若△B1O1C1的两个顶点恰好落在抛物线上,请求点B1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
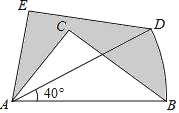
【题目】如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕A逆时针方向旋转40°得到△ADE,点B经过的路径为弧BD,则图中阴影部分(△ABC以外的部分)的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.

(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
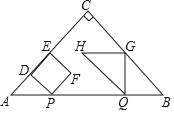
【题目】△ABC是等腰直角三角形,∠ACB=90°,AB=8cm,动点P、Q以2cm/s的速度分别从点A、B同时出发,点P沿A到B向终点B运动,点Q沿B到A向终点A运动,过点P作PD⊥AC于点D,以PD为边向右侧作正方形PDEF,过点Q作QG⊥AB,交折线BC﹣CA于点G与点C不重合,以QG为边作等腰直角△QGH,且点G为直角顶点,点C、H始终在QG的同侧,设正方形PDEF与△QGH重叠部分图形的面积为S(cm2),点P运动的时间为t(s)(0<t<4).
(1)当点F在边QH上时,求t的值.
(2)点正方形PDEF与△QGH重叠部分图形是四边形时,求S与t之间的函数关系式;
(3)当FH所在的直线平行或垂直AB时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
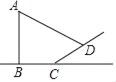
【题目】如图所示,小明准备测量学校旗杆AB的高度,他发现阳光下,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,测得水平地面上的影长BC=20m,斜坡坡面上的影长CD=8m,太阳光线AD与水平地面成锐角为26°,斜坡CD与水平地面所成的锐角为30°,求旗杆AB的高度(精确到1m).(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 和正方形
和正方形![]() 的顶点
的顶点![]() 在
在![]() 轴上,顶点
轴上,顶点![]() ,
,![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 边上,反比例函数
边上,反比例函数![]() 的图象经过点
的图象经过点![]() 、
、![]() 和边
和边![]() 的中点
的中点![]() .若
.若![]() ,则正方形
,则正方形![]() 的面积为( )
的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com