
【题目】已知,在△ABC中,∠ACB=30°
(1)如图1,当AB=AC=2,求BC的值;
(2)如图2,当AB=AC,点P是△ABC内一点,且PA=2,PB=![]() ,PC=3,求∠APC的度数;
,PC=3,求∠APC的度数;
(3)如图3,当AC=4,AB=![]() (CB>CA),点P是△ABC内一动点,则PA+PB+PC的最小值为 .
(CB>CA),点P是△ABC内一动点,则PA+PB+PC的最小值为 .

【答案】(1)BC=2![]() ;(2)∠APC=120°;(3)
;(2)∠APC=120°;(3)![]() .
.
【解析】
作AP⊥BC于P,因为AC=2,∠C=30°,利用![]() 求得PC,再利用垂径定理得BP=PC,即可求解.
求得PC,再利用垂径定理得BP=PC,即可求解.
因为AB=AC,∠C=30°,所以∠BAC=120°,将△APB绕点A逆时针旋转120°得到△QAC,所以![]() ,因为∠PAQ=120°,所以PQ=2
,因为∠PAQ=120°,所以PQ=2 ![]() ,PQ2+PC2=QC2,∠QPC=90°,APQ=30°,∠APC=∠APQ +∠QPC代入即可求解.
,PQ2+PC2=QC2,∠QPC=90°,APQ=30°,∠APC=∠APQ +∠QPC代入即可求解.
将△BCP绕点C逆时针旋转60°得到△CB′P′,连接PP′,AB′,则∠ACB′=90°,因为PA+PB+PC=PA+PP′+P′B′,所以当A,P,P′,B′共线时,PA+PB+PC的值最小,最小值=AB′的长,再根据勾股定理即可求解.
解:(1)如图1中,作AP⊥BC于P.
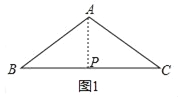
∵AB=AC,AP⊥BC,
∴BP=PC,
在Rt△ACP中,∵AC=2,∠C=30°,
∴PC=ACcos30°=![]() ,
,
∴BC=2PC=2![]() .
.
(2)如图2中,
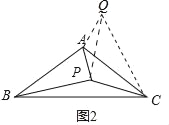
∵AB=AC,∠C=30°,
∴∠BAC=120°,
将△APB绕点A逆时针旋转120°得到△QAC.
∴PA=AQ=2,PB=QC=![]() ,
,
∵∠PAQ=120°,
∴PQ=2![]() ,
,
∴PQ2+PC2=QC2,
∴∠QPC=90°,
∵∠APQ=30°,
∴∠APC=30°+90°=120°.
(3)如图3中,将△BCP绕点C逆时针旋转60°得到△CB′P′,连接PP′,AB′,则∠ACB′=90°.
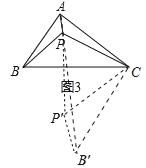
∵PA+PB+PC=PA+PP′+P′B′,
∴当A,P,P′,B′共线时,PA+PB+PC的值最小最小值=AB′的长,
p>由AB=∴AB′=![]() =
=![]() .
.
故答案为![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两位同学在一次实验中统计了某一结果出现的频率,给出的统计图如图所示,则 符合这一结果的实验可能是( )

A. 掷一枚正六面体的骰子,出现6点的概率
B. 掷一枚硬币,出现正面朝上的概率
C. 任意写出一个整数,能被2整除的概率
D. 一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+3)x+m2=0有两个不相等的实数根,
(1)求m的取值范围
(2)若α,β是方程的两个实数根,且满足![]() =﹣1,求m的值.
=﹣1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
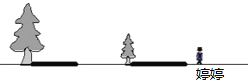
【题目】两棵树(大树和小树)在一盏路灯下的影子如图所示
(1)确定路灯灯泡的位置(用点P表示)和表示婷婷的影长的线段(用线段AB表示).
(2)若小树高为2m,影长为4m;婷婷高1.5m,影长为4.5米,且婷婷距离小树10米,试求出路灯灯泡的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
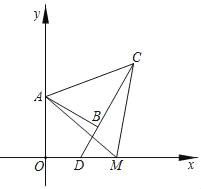
【题目】如图,在平面直角坐标系中,已知A(0,2),M(m,0)且m>0,分别以AO、AM为边在∠AOM内部作等边△AOB和等边△AMC,连接CB并延长交x轴于点D,则C点的横坐标的值为( )
A. ![]() m+
m+![]() B.
B. ![]() m+
m+![]() C.
C. ![]() m+
m+![]() D.
D. ![]() m+
m+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一张边长为40 cm的正方形硬纸板,进行适当的裁剪,折成一个长方体盒子(纸板的厚度忽略不计).
(1)如图,若在正方形硬纸板的四角各剪掉一个同样大小的正方形,将剩余部分折成一个无盖的长方体盒子.

①要使折成的长方体盒子的底面积为484 cm2,那么剪掉的正方形的边长为多少?
②折成的长方体盒子的侧面积是否有最大值?如果有,求出这个最大值和此时剪掉的正方形的边长;如果没有,说明理由.
(2)若在正方形硬纸板的四周剪掉一些矩形(即剪掉的矩形至少有一条边在正方形硬纸板的边上),将剩余部分折成一个有盖的长方体盒子.若折成的一个长方体盒子的表面积为550 cm2,求此时长方体盒子的长、宽、高(只需求出符合要求的一种情况).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是⊙O的一个内接三角形,∠B=60°,AC=6,图中阴影部分面积记为S,则S的最小值( )

A. 8π﹣9![]() B. 8π﹣6
B. 8π﹣6![]() C. 8π﹣3
C. 8π﹣3![]() D. 8π﹣2
D. 8π﹣2![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com