【题目】如图，△ABC是⊙O的一个内接三角形，∠B＝60°，AC＝6，图中阴影部分面积记为S，则S的最小值（ ）
A. 8π﹣9
B. 8π﹣6 C. 8π﹣3 D. 8π﹣2
七星图书口算速算天天练系列答案科目：初中数学 来源： 题型：
【题目】如图，BC是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆CD的顶端D处有一探射灯，射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°（图中的点A、B、C、D、M、N均在同一平面内，CM∥AN）．
（1）求灯杆CD的高度；
（2）求AB的长度（结果精确到0.1米）．（参考数据：
=1.73．sin37°≈060，cos37°≈0.80，tan37°≈0.75）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，在△ABC中，∠ACB＝30°
（1）如图1，当AB＝AC＝2，求BC的值；
（2）如图2，当AB＝AC，点P是△ABC内一点，且PA＝2，PB＝
，PC＝3，求∠APC的度数；
（3）如图3，当AC＝4，AB＝
（CB＞CA），点P是△ABC内一动点，则PA+PB+PC的最小值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
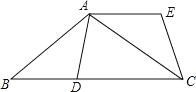
【题目】如图，在△ABC 中，AB＝AC．D 是 BC 上一点，且 AD＝BD．将△ABD 绕点 A 逆时针旋转得到△ACE．
（1）求证：AE∥BC；
（2）连结 DE，判断四边形 ABDE 的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某部门为了解本市2018年推荐生测试运动与健康、审美与表现两科的等级情况，从推荐生中随机抽取了400名学生的这两科等级成绩，并将得到的数据绘制成了如图统计图．
（1）在抽取的400名学生中，运动与健康成绩为A等级的人数是 ；
（2）在抽取的400名学生中，审美与表现成绩为B等级的人数是 ；
（3）若2018年该市共有推荐生10000名，估计运动与健康成绩为C、D等级的人数约为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
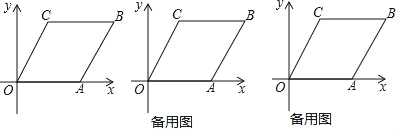
【题目】如图，在边长为5的菱形OABC中，sin∠AOC＝
，O为坐标原点，A点在x轴的正半轴上，B，C两点都在第一象限．点P以每秒1个单位的速度沿O→A→B→C→O运动一周，设运动时间为t（秒）．请解答下列问题：
（1）当CP⊥OA时，求t的值；
（2）当t＜10时，求点P的坐标（结果用含t的代数式表示）；
（3）以点P为圆心，以OP为半径画圆，当⊙P与菱形OABC的一边所在直线相切时，请直接写出t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
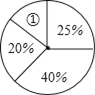
【题目】物理兴趣小组20位同学在实验操作中的得分情况如下表：（Ⅰ）求这组数据的众数、中位数；（Ⅱ）求这组数据的平均数；（Ⅲ）将此次操作得分按人数制成如图所示的扇形统计图．扇形①的圆心角度数是多少？
得分（分） | 10 | 9 | 8 | 7 |
人数（人） | 5 | 8 | 4 | 3 |
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有一个二次函数的图象，三位同学分别说出了它的一些特点：
甲：对称轴为直线x=4
乙：与x轴两个交点的横坐标都是整数．
丙：与y轴交点的纵坐标也是整数，且以这三个点为顶点的三角形面积为3．请你写出满足上述全部特点的一个二次函数解析式__________________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
