
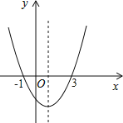
【题目】如图,二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,给出的下列6个结论:
①ab<0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③4a+2b+c<0;
④当x>1时,y随x值的增大而增大;
⑤当y>0时,﹣1<x<3;
⑥3a+2c<0.
其中不正确的有_____.
【答案】⑤
【解析】
①由图象可知,a>0,b<0,则问题可解;②根据图象与x轴交点,问题可解;③由图象可知,当x=2时,对应的点在x轴下方,x=2时,函数值为负;④由图象可知,抛物线对称轴为直线x=1,当x>1时,y随x值的增大而增大;⑤由图象可知,当y>0时,对应x>3或x<-1;⑥根据对称轴找到ab之间关系,再代入a﹣b+c=0,问题可解.综上即可得出结论.
解:①∵抛物线开口向上,对称轴在y轴右侧,与y轴交于负半轴,
∴a>0,﹣![]() >0,c<0,
>0,c<0,
∴b<0,
∴ab<0,说法①正确;
②二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,
∴方程ax2+bx+c=0的根为x1=﹣1,x2=3,说法②正确;
③∵当x=2时,函数y<0,
∴4a+2b+c<0,说法③正确;
④∵抛物线与x轴交于(﹣1,0)、(3,0)两点,
∴抛物线的对称轴为直线x=1,
∵图象开口向上,
∴当x>1时,y随x值的增大而增大,说法④正确;
⑤∵抛物线与x轴交于(﹣1,0)、(3,0)两点,且图象开口向上,
∴当y<0时,﹣1<x<3,说法⑤错误;
⑥∵当x=﹣1时,y=0,
∴a﹣b+c=0,
∴抛物线的对称轴为直线x=1=﹣![]() ,
,
∴b=﹣2a,
∴3a+c=0,
∵c<0,
∴3a+2c<0,说法⑥正确.
故答案为⑤.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=
的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=![]() 的点P的个数是( )
的点P的个数是( )

A.0B.4C.8D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
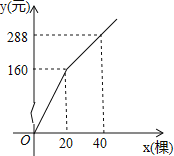
【题目】为更新树木品种,某植物园计划购进甲、乙两个品种的树苗栽植培育若计划购进这两种树苗共41棵,其中甲种树苗的单价为6元/棵,购买乙种树苗所需费用y(元)与购买数量x(棵)之间的函数关系如图所示.
(1)求出y与x的函数关系式;
(2)若在购买计划中,乙种树苗的数量不超过35棵,但不少于甲种树苗的数量.请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 | 86 | 92 | 80 | 90 |
面试 | 90 | 88 | 94 | 84 |
(1)这4名选手笔试成绩的中位数是 分,面试的平均数是 分.
(2)该公司规定:笔试、面试分别按40%,60%的比例计入总分,且各项成绩都不得低于85分. 根据规定,请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A(-3,y1)、B(-1,y2)、C(1,y3)三点都在反比例函数y=![]() (k>0)的图象上,则y1、y2、y3的大小关系是( )
(k>0)的图象上,则y1、y2、y3的大小关系是( )
A. y1>y2>y3B. y3>y1>y2C. y3>y2>y1D. y2>y1>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
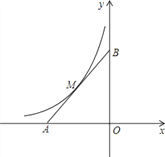
【题目】已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数![]() 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM.
(1)求点M的坐标;
(2)求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP.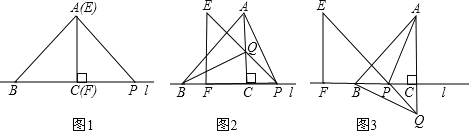
(1)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系,请证明你的猜想;
(2)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP,BQ.你认为(1)中所猜想的BQ与AP的数量关系还成立吗?若成立,给出证明;若不成立,请说明理由;
(3)若AC=BC=4,设△EFP平移的距离为x,当0≤x≤8时,△EFP与△ABC重叠部分的面积为S,请写出S与x之间的函数关系式,并求出最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两个不透明的口袋中,分别有4个和3个大小、材质完全相同的小球,其中甲口袋中的小球上标有数字0,1,2,3,乙口袋中的小球上分别标有数字1,2,3,先从甲口袋中随机摸出一个小球,记下数字为![]() ,再从乙口袋中随机摸出一个小球,记下数字为
,再从乙口袋中随机摸出一个小球,记下数字为![]() .
.
(1)请用列表法或画树状图的方法表示出所有![]() 可能的结果;
可能的结果;
(2)规定:若![]() 都是方程
都是方程![]() 的解时,则小明获胜;若
的解时,则小明获胜;若![]() 都不是方程
都不是方程![]() 的解时,则小宇获胜,问他们两人谁获胜的概率大?
的解时,则小宇获胜,问他们两人谁获胜的概率大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com