
【题目】若A(-3,y1)、B(-1,y2)、C(1,y3)三点都在反比例函数y=![]() (k>0)的图象上,则y1、y2、y3的大小关系是( )
(k>0)的图象上,则y1、y2、y3的大小关系是( )
A. y1>y2>y3B. y3>y1>y2C. y3>y2>y1D. y2>y1>y3
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】某文具商店销售学习用品,已知某品牌钢笔的进价是20元,销售过程发现,每月销量y支与销售单价x元(x为正整数)之间满足一次函数关系,且每支钢笔的售价不低于进价,也不高于35元,下表是y与x之间的对应数据:
销售单价x(元) | … | 22 | 24 | 30 | … |
月销量y(只) | … | 92 | 84 | 60 | … |
(1)求y与x的函数关系式并直接写出自变量x的取值范围.
(2)每支钢笔的售价定为多少元时,月销售利润恰为600元?
(3)每支钢笔的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
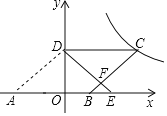
【题目】如图,在平面直角坐标系中,O为坐标原点,ABCD的边AB在x轴上,顶点D在y轴的正半轴上,点C在第一象限.将△AOD沿y轴翻折,使点A落在x轴上的点E处,点B恰好为OE的中点,DE与BC交于点F.若y=![]() (k≠0)图象经过点C,且S△BEF=
(k≠0)图象经过点C,且S△BEF=![]() ,则k的值为_____.
,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
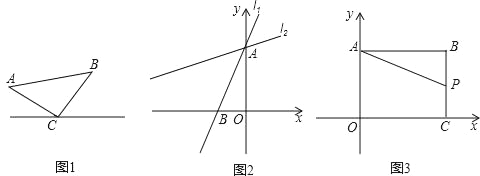
【题目】建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
实践操作:过点A作AD⊥l于点D,过点B作BE⊥l于点E,求证:△CAD≌△BCE.
模型应用:(1)如图2,在直角坐标系中,直线l1:y=![]() x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于第一象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0),B(4,0),C(0,2)三点.
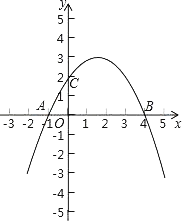
(1)求该二次函数的解析式;
(2)设点D是在x轴上方的二次函数图象上的点,且△DAB的面积为5,求出所有满足条件的点D的坐标;
(3)能否在抛物线上找点P,使∠APB=90°?若能,请直接写出所有满足条件的点P;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
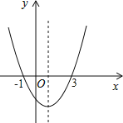
【题目】如图,二次函数y=ax2+bx+c的图象经过(﹣1,0)(3,0)两点,给出的下列6个结论:
①ab<0;
②方程ax2+bx+c=0的根为x1=﹣1,x2=3;
③4a+2b+c<0;
④当x>1时,y随x值的增大而增大;
⑤当y>0时,﹣1<x<3;
⑥3a+2c<0.
其中不正确的有_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
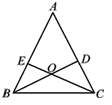
【题目】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列四个条件:
①∠EBO=∠DCO;②BE=CD;③OB=OC;④OE=OD.
从上述四个条件中,选取两个条件,不能判定△ABC是等腰三角形的是:( )
A. ①②B. ①③C. ③④D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以△ABC的边AB为直径作⊙O,点C在⊙O上,BD是⊙O的弦,∠A=∠CBD,过点C作CF⊥AB于点F,交BD于点G,过C作CE∥BD交AB的延长线于点E.
(1)求证:CE是⊙O的切线;
(2)求证:CG=BG;
(3)若∠DBA=30°,CG=4,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间甲乙两商场搞促销活动,甲商场的方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”“20元”“30元”“50元”,顾客每消费满300元就可从箱子里不放回地摸出2个球,根据两个小球所标金额之和可获相应价格的礼品;乙商场的方案是:在一个不透明的箱子里放2个完全相同的小球,球上分别标“5元”“30元”,顾客每消费满100元,就可从箱子里有放回地摸出1个球,根据小球所标金额可获相应价格的礼品.某顾客准备消费300元.
(1)请用画树状图或列表法,求出该顾客在甲商场获得礼品的总价值不低于50元的概率;
(2)判断该顾客去哪个商场消费使获得礼品的总价值不低于50元机会更大?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com