
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0),B(4,0),C(0,2)三点.
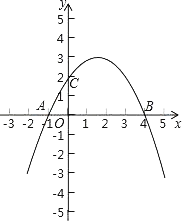
(1)求该二次函数的解析式;
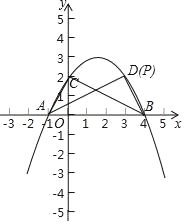
(2)设点D是在x轴上方的二次函数图象上的点,且△DAB的面积为5,求出所有满足条件的点D的坐标;
(3)能否在抛物线上找点P,使∠APB=90°?若能,请直接写出所有满足条件的点P;若不能,请说明理由.
【答案】(1)![]() ;(2)点D的坐标为(0,2)或(3,2);(3)能,满足条件的点P的坐标为(0,2)或(3,2).
;(2)点D的坐标为(0,2)或(3,2);(3)能,满足条件的点P的坐标为(0,2)或(3,2).
【解析】
(1)根据点A、B、C的坐标,利用待定系数法即可求出二次函数的解析式;
(2)设点D的纵坐标为m(m>0),根据三角形的面积公式结合△DAB的面积为5,即可得出关于m的一元一次方程,解之即可得出m的值,再利用二次函数图象上点的坐标特征即可求出点D的坐标;
(3)假设成立,等点P与点C重合时,可利用勾股定理求出AP、BP的长度,由AP2+BP2=AB2可得出此时∠APB=90°,再利用二次函数图象的对称性即可找出点P的另一坐标,此题得解.
解:(1)∵二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0)、B(4,0)、C(0,2)三点,
∴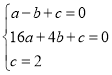 ,解得:
,解得: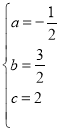 ,
,
∴该二次函数的解析式为![]() .
.
(2)设点D的纵坐标为m(m>0),
则![]() ,
,
∴m=2.
当y=2时,有![]() ,
,
解得:x1=0,x2=3,
∴满足条件的点D的坐标为(0,2)或(3,2).
(3)假设能,当点P与点C重合时,
有![]() ,
,
∵![]() ,即AP2+BP2=AB2,
,即AP2+BP2=AB2,
∴∠APB=90°,
∴假设成立,点P的坐标为(0,2).
由对称性可知:当点P的坐标为(3,2)时,∠APB=90°.
故满足条件的点P的坐标为(0,2)或(3,2).


科目:初中数学 来源: 题型:
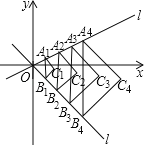
【题目】如图,在平面直角坐标系中,△A1B1C1,△A2B2C2,△A3B3C3,…,△AnBnCn均为等腰直角三角形,且∠C1=∠C2=∠C3=…=∠Cn=90°,点A1,A2,A3,…,An和点B1,B2,B3,…,Bn分别在正比例函数y=![]() x和y=﹣x的图象上,且点A1,A2,A3,…,An的横坐标分别为1,2,3…n,线段A1B1,A2B2,A3B3,…,AnBn均与y轴平行.按照图中所反映的规律,则△AnBnCn的顶点Cn的坐标是____.(其中n为正整数)
x和y=﹣x的图象上,且点A1,A2,A3,…,An的横坐标分别为1,2,3…n,线段A1B1,A2B2,A3B3,…,AnBn均与y轴平行.按照图中所反映的规律,则△AnBnCn的顶点Cn的坐标是____.(其中n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)求证:△DOE≌△BOF;
(2)若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,∠AOB=90°,AO=3BO,OB在x轴上,将Rt△AOB绕点O顺时针旋转至△RtA'OB',其中点B'落在反比例函数y=﹣![]() 的图象上,OA'交反比例函数y=
的图象上,OA'交反比例函数y=![]() 的图象于点C,且OC=2CA',则k的值为( )
的图象于点C,且OC=2CA',则k的值为( )

A. 4 B. ![]() C. 8 D. 7
C. 8 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A(-3,y1)、B(-1,y2)、C(1,y3)三点都在反比例函数y=![]() (k>0)的图象上,则y1、y2、y3的大小关系是( )
(k>0)的图象上,则y1、y2、y3的大小关系是( )
A. y1>y2>y3B. y3>y1>y2C. y3>y2>y1D. y2>y1>y3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师从学校出发,到距学校![]() 的某商场去给学生买奖品,他先步行了
的某商场去给学生买奖品,他先步行了![]() 后,换骑上了共享单车,到达商场时,全程总共刚好花了
后,换骑上了共享单车,到达商场时,全程总共刚好花了![]() .已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).
.已知王老师骑共享单车的平均速度是步行速度的3倍(转换出行方式时,所需时间忽略不计).
(1)求王老师步行和骑共享单车的平均速度分别为多少?
(2)买完奖品后,王老师原路返回,为按时上班,路上所花时间最多只剩10分钟,若王老师仍采取先步行,后换骑共享单车的方式返回,问:他最多可步行多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
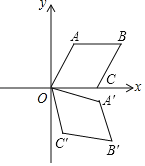
【题目】如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,以AB为直径的⊙O交AC于点D,点E在BC上,连接BD,DE,∠CDE=∠ABD.
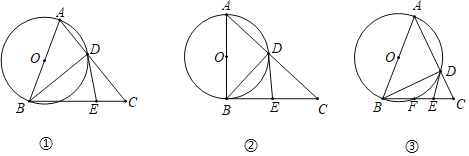
(1)求证:DE是⊙O的切线.
(2)如图②,当∠ABC=90°时,线段DE与BC有什么数量关系?请说明理由.
(3)如图③,若AB=AC=10,sin∠CDE=![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com