
【题目】在20km越野赛中,甲乙两选手的行程y(单位:km)随时间x(单位:h)变化的图象如图所示,根据图象信息,下列说法:①两人相遇前,甲速度一直小于乙速度;②出发后1小时,两人行程均为10km;③出发后1.5小时,甲的行程比乙多3km;④甲比乙先到达终点.其中正确的说法是_________(填序号).
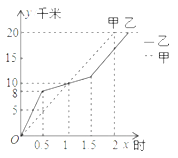
【答案】②③④
【解析】
根据相遇前的图像乙的速度有变化,没有都大于甲的速度,即可判断①,根据出发后1小时,甲乙相遇,可判断②,求出甲路程与时间的函数,及乙在0.5到1.5小时这段时间的函数,即可判断③,由图像甲先到到达20km处,知甲先到终点,故可判断④.
根据相遇前的图像乙的速度有变化,没有都大于甲的速度,∴①错误;
根据出发后1小时,甲乙相遇,∴②正确,
利用甲函数经过原点与(1,10)求出甲路程与时间的函数为y=10x,
乙在0.5到1.5小时这段时间的函数经过(0.5,8),(1,10),求出这段时间的函数为y=4x+6,
∴1.5h时,甲的路程为15km,乙的路程为12km, 甲的行程比乙多3km,故③正确,
由图像甲先到到达20km处,知甲先到终点,故可判断④正确.
故填②③④


科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水品质的需求越来越高,某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A,B两种型号的净水器共50台进行试销,其中A型净水器为x台,购买资金不超过9.8万元,试销时A型净水器每台售价2500元,B型净水器每台售价2180元,公司决定从销售A型净水器的利润中按每台捐献a元作为公司帮扶贫困村饮水改造资金.若公司售完50台净水器并捐献扶贫资金后获得的最大利润不低于20200元但不超过23000元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…,依次进行下去,则点A2019的坐标为( )
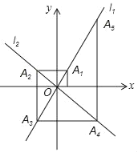
A.(21009,21010)B.(﹣21009,21010)
C.(21009,﹣21010)D.(﹣21009,﹣21010)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为( )
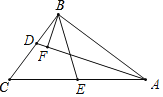
A.19°B.33°C.34°D.43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更新树木品种,某植物园计划购进甲、乙两个品种的树苗栽植培育若计划购进这两种树苗共41棵,其中甲种树苗的单价为6元/棵,购买乙种树苗所需费用y(元)与购买数量x(棵)之间的函数关系如图所示.
(1)求出y与x的函数关系式;
(2)若在购买计划中,乙种树苗的数量不超过35棵,但不少于甲种树苗的数量.请设计购买方案,使总费用最低,并求出最低费用.
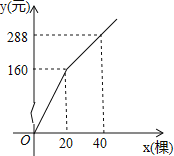
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业设计了一款工艺品,每件的成本是50元,为了合理定价,投放市场进行试销.据市场调查,销售单价是100元时,每天的销售量是50件,而销售单价每降低1元,每天就可多售出5件,但要求销售单价不得低于成本.
![]() 求出每天的销售利润
求出每天的销售利润![]() 元
元![]() 与销售单价
与销售单价![]() 元
元![]() 之间的函数关系式;
之间的函数关系式;
![]() 求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
求出销售单价为多少元时,每天的销售利润最大?最大利润是多少?
![]() 如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?
如果该企业要使每天的销售利润不低于4000元,且每天的总成本不超过7000元,那么销售单价应控制在什么范围内?![]() 每天的总成本
每天的总成本![]() 每件的成本
每件的成本![]() 每天的销售量
每天的销售量![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 | 86 | 92 | 80 | 90 |
面试 | 90 | 88 | 94 | 84 |
(1)这4名选手笔试成绩的中位数是 分,面试的平均数是 分.
(2)该公司规定:笔试、面试分别按40%,60%的比例计入总分,且各项成绩都不得低于85分. 根据规定,请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
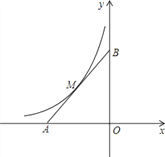
【题目】已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数![]() 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM.
(1)求点M的坐标;
(2)求直线AB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(4,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=3时,这两个二次函数的最大值之和等于()
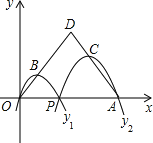
A.![]() B.
B.![]() C.3D.4
C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com