
����Ŀ����������ˮƽ����ߣ����Ƕ���ˮƷ�ʵ�����Խ��Խ�ߣ�ij��˾�����г��������A��B�����ͺŵľ�ˮ����ÿ̨A�;�ˮ����ÿ̨B�;�ˮ�����۶�200Ԫ����5��Ԫ����A�;�ˮ������4.5��Ԫ����B�;�ˮ�����������
��1����ÿ̨A�͡�B�;�ˮ���Ľ��۸��Ƕ���Ԫ��
��2���ù�˾�ƻ�����A��B�����ͺŵľ�ˮ����50̨��������������A�;�ˮ��Ϊx̨�������ʽ���9.8��Ԫ������ʱA�;�ˮ��ÿ̨�ۼ�2500Ԫ��B�;�ˮ��ÿ̨�ۼ�2180Ԫ����˾����������A�;�ˮ���������а�ÿ̨����aԪ��Ϊ��˾���ƶ������ˮ�����ʽ�����˾����50̨��ˮ��������ƶ�ʽ���õ����������20200Ԫ��������23000Ԫ����a��ȡֵ��Χ��
���𰸡���1��ÿ̨A�͡�B�;�ˮ���Ľ��۷ֱ���2000Ԫ��1800Ԫ����2��a��ȡֵ��Χ��20��a��90��
��������
��1��������������г���Ӧ�ķ�ʽ���̣��Ӷ����Խ���⣻
��2����������������x��ȡֵ��Χ��������x�ĺ�����ϵʽ��Ȼ�����һ�κ��������ʼ��ɽ���⣮
��1����ÿ̨A�͵Ľ���ΪmԪ��
![]() ��
��
��ã�m��2000��
�����飬m��2000��ԭ��ʽ���̵Ľ⣬
��m��200��1800��
��ÿ̨A�͡�B�;�ˮ���Ľ��۷ֱ���2000Ԫ��1800Ԫ��
��2��2000x+1800��50��x����98000��
��ã�x��40��
�蹫˾����50̨��ˮ���������õ�����ΪwԪ��
w����2500��2000��x+��2180��1800����50��x����ax����120��a��x+19000��
��a��120ʱ��w��19000�������⣬
��a��120ʱ��120��a��0����x��40ʱ��wȡ�����ֵ��
��20200��40��120��a��+19000��23000��
��ã�20��a��90��
��a��ȡֵ��Χ��20��a��90��


 �����������Ů��ͯ������ϵ�д�
�����������Ů��ͯ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�![]() Ϊ����ԭ�㣬ƽ���ı���
Ϊ����ԭ�㣬ƽ���ı���![]() �ı�
�ı�![]() ��
��![]() ���������ϣ�����
���������ϣ�����![]() ��
��![]() ���������ϣ�����
���������ϣ�����![]() ��ͼ����
��ͼ����![]() ����
����![]() ���߶�
���߶�![]() �Ͻӽ���
�Ͻӽ���![]() �����ȷֵ㣬
�����ȷֵ㣬![]() ������Ϊ��
��������![]() ����
����![]() ǡ�����߶�
ǡ�����߶�![]() ���е㣬����
���е㣬����![]() ��
��![]() ���ڵ�
���ڵ�![]() �����ı���
�����ı���![]() ������ǣ���
������ǣ���
A.![]() B.5C.
B.5C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�����������������������̽��
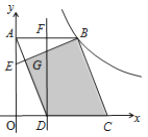
���壺��ͼ1����������![]() �У���
�У���![]() Ϊֱ������Բ
Ϊֱ������Բ![]() ����
����![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��
Ϊ�뾶��![]() �����Բ
�����Բ![]() ���ڵ�
���ڵ�![]() .���dzƵ�
.���dzƵ�![]() Ϊ������
Ϊ������![]() ��һ��������������������Ķ����߶���������
��һ��������������������Ķ����߶���������![]() ������λ�ù�ϵ����������ϵ�������в�������������ֵ��̽����
������λ�ù�ϵ����������ϵ�������в�������������ֵ��̽����
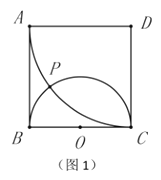
����̽������ͼ2������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ��Բ
Ϊ��Բ![]() �����ߣ�
�����ߣ�
֤��������![]() ��
��
����ͼ��֪��![]() ��
��
��![]() ��
��
![]()
![]() ����
����![]() �ǰ�Բ
�ǰ�Բ![]() �����ߣ�
�����ߣ�
��������
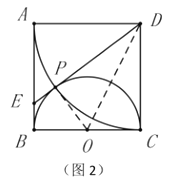
��1����ͼ3����ͼ2�Ļ����ϣ�����![]() .���ж�
.���ж�![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
��2���ڣ�1���������£���ֱ��д���߶�![]() ֮���������ϵ��
֮���������ϵ��
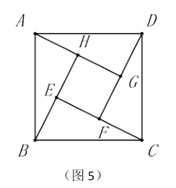
��3����ͼ4����֪��![]() Ϊ������
Ϊ������![]() ��һ���������������
��һ���������������![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ������
������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ����д��
�����![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
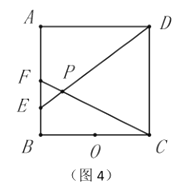
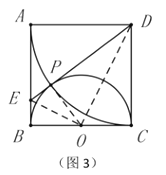
��4����ͼ5����֪��![]() Ϊ������
Ϊ������![]() ���ĸ����������������
���ĸ����������������![]() ��ǡ�õõ�һ�����������ˬ��ͼ���������ͼ�Σ�̽����ֱ��д��һ����ȫ�ȵļ���ͼ�����֮���������ϵ��
��ǡ�õõ�һ�����������ˬ��ͼ���������ͼ�Σ�̽����ֱ��д��һ����ȫ�ȵļ���ͼ�����֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���![]() �У�
�У�![]() Ϊ
Ϊ![]() �е㣬��
�е㣬��![]() Ϊ����������
����������![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ���ڱ�
���ڱ�![]() ��ȡ��
��ȡ��![]() ʹ
ʹ![]() ����
����![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
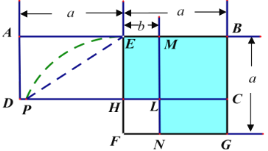
��1���������ø�ͼ����ƽ���ʽ��![]() ��
��
��2�����Ե�![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��Բ�����߶�
Ϊ�뾶��Բ�����߶�![]() �ڵ�
�ڵ�![]() ������
������![]() ������
������![]() ��ͬһֱ���ϣ���
��ͬһֱ���ϣ���![]() ��ֵ��
��ֵ��
��3����![]() �����Ϊ
�����Ϊ![]() ��ͼ���ı���
��ͼ���ı���![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ1��������ABCD�Ƶ�A��ʱ����ת45����õ�������AB1C1D1����B1C1��CD���ڵ�O����ͼ����Ӱ���ֵ�����ǣ�������
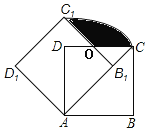
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ijѧУΪ���˽���꼶ѧ���������������ȡ�˲���ѧ�����������ܲ��ԣ�ѧ���IJ��Գɼ������ࣺA�����㣻B�����ã�C���ϸ�D���ϸ����ѧ���ijɼ����Ƴ�����������������ͳ��ͼ�������ͳ��ͼ����������⣺
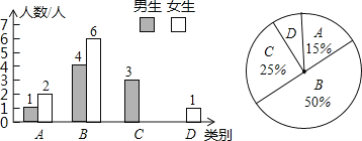
��1���ε����ѧ����������
��2���ɼ�ΪC��Ů����______�ˣ��ɼ�ΪD��������______�ˣ�
��3������ͳ��ͼ�гɼ�ΪD��ѧ������Ӧ�����ε�Բ�ĽǶ���Ϊ______��
��4����ȫ����ͳ��ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�Ƿ���������![]() ͼ���ϵ����㣬����A��AC��y�ᣬ����ΪC����OB�ڵ�D����DΪOB���е㣬����ABO�����Ϊ4����k��ֵΪ______.
ͼ���ϵ����㣬����A��AC��y�ᣬ����ΪC����OB�ڵ�D����DΪOB���е㣬����ABO�����Ϊ4����k��ֵΪ______.
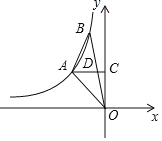
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������Ϊ�˷�ƶ����������ũ����ֳС��Ϻ����ͼ��������˳����AN��AM��AN��3![]() m��AM��10m����MAN��45�㣩����8m�����������һ����ֳˮ���ı���ABCD�������߲���Ҫ������AB��CD����C��90�㣮��BC��xm���ı���ABCD���ΪS��m2����
m��AM��10m����MAN��45�㣩����8m�����������һ����ֳˮ���ı���ABCD�������߲���Ҫ������AB��CD����C��90�㣮��BC��xm���ı���ABCD���ΪS��m2����
��1�����S����x�ĺ�������ʽ��x��ȡֵ��Χ��
��2��xΪ��ֵʱ��Χ�ɵ���ֳˮ���������������Ƕ��٣�
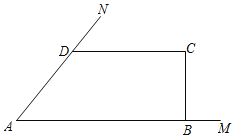
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����20kmԽҰ���У�������ѡ�ֵ��г�y����λ��km����ʱ��x����λ��h���仯��ͼ����ͼ��ʾ������ͼ����Ϣ������˵��������������ǰ�����ٶ�һֱС�����ٶȣ��ڳ�����1Сʱ�������г̾�Ϊ10km���۳�����1.5Сʱ�����г̱��Ҷ�3km���ܼױ����ȵ����յ㣮������ȷ��˵����_________������ţ���
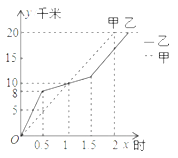
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com