
【题目】如图,在矩形![]() 中,
中,![]() 为
为![]() 中点,以
中点,以![]() 为边作正方形
为边作正方形![]() ,边
,边![]() 交
交![]() 于点
于点![]() .在边
.在边![]() 上取点
上取点![]() 使
使![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
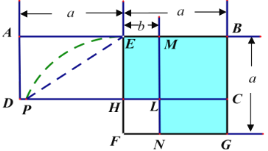
(1)请你利用该图解释平方差公式:![]() .
.
(2)现以点![]() 为圆心,
为圆心,![]() 为半径作圆弧交线段
为半径作圆弧交线段![]() 于点
于点![]() ,连接
,连接![]() .若点
.若点![]() 在同一直线上,求
在同一直线上,求![]() 的值?
的值?
(3)记![]() 的面积为
的面积为![]() ,图中四边形
,图中四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)3;(3)![]()
【解析】
(1)分别利用a和b表示出S矩形ADLM和阴影部分的面积,然后根据S矩形ADLM=S矩形ADHE+S矩形EHLM =S矩形EHCB+S矩形LNGC=S阴影,即可证出结论;
(2)连接AG,利用平行证出△AML∽△GNL,然后列出比例式即可求出结论;
(3)连接PF,则PF=EF=a,HF=b,且a=3b,根据面积公式求出![]() 和
和![]() 即可求出结论.
即可求出结论.
解:(1)由图可知:AE=BE=BG=a,EM=b
由题已知:四边形ADLM、ADHE、EHCB、EHLM、LNGC都为矩形,四边形EFGB、HFNL都为正方形,CG=EM=b,BC=a-b且S矩形ADHE=S矩形EHCB,S矩形EHLM= S矩形LNGC
∴S矩形ADLM =AD·AM= BC·AM=(a-b)(a+b)
图中阴影部分的面积=S正方形EFGB-S正方形HFNL=a2-b2
∵S矩形ADLM=S矩形ADHE+S矩形EHLM =S矩形EHCB+S矩形LNGC=S阴影
∴(a-b)(a+b)= a2-b2
(2)连接AG,由题意可知,AG必过点L,
∵AM∥GN
∴△AML∽△GNL
∴![]()
即![]()
解得:a=3b
∴![]() =3;
=3;
(3)连接PF,则PF=EF=a,HF=b,且a=3b
∴PH=![]()
∴![]() =
=![]() PH·EH=
PH·EH=![]()
![]() ·(a-b)=
·(a-b)=![]()
![]() =a(a-b)=
=a(a-b)=![]()
∴![]() =
=![]()



 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
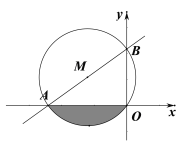
【题目】一次函数![]() 的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且
的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且![]() △OAB的外接圆的圆心M的横坐标为-3.
△OAB的外接圆的圆心M的横坐标为-3.
(1)求一次函数的解析式;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解九年级学生的身体素质测试情况,随机抽取了该市九年级部分学生的身体素质测试成绩作为样本,按![]() (优秀),
(优秀),![]() (良好),
(良好),![]() (合格),
(合格),![]() (不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:

(1)此次共调查了多少名学生?
(2)将条形统计图补充完整,并计算扇形统计图中“![]() ”部分所对应的圆心角的度数.
”部分所对应的圆心角的度数.
(3)该市九年级共有9000名学生参加了身体素质测试,估计测试成绩在良好以上(含良好)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
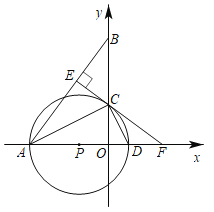
【题目】如图,△AOB中,A(-8,0),B(0,![]() ),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴交于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F.
),AC平分∠OAB,交y轴于点C,点P是x轴上一点,⊙P经过点A、C,与x轴交于点D,过点C作CE⊥AB,垂足为E,EC的延长线交x轴于点F.
(1)求证:EF为⊙P的切线;
(2)求⊙P的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() .
.
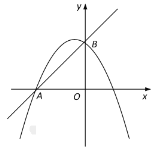
(1)求![]() 满足的关系式及
满足的关系式及![]() 的值;
的值;
(2)当![]() 时,求抛物线解析式,并直接写出当
时,求抛物线解析式,并直接写出当![]() 时
时![]() 的取值范围.
的取值范围.
(3)当![]() 时,若
时,若![]() 的函数值随
的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
(4)如图,当![]() 时,在第二象限的抛物线上找点
时,在第二象限的抛物线上找点![]() ,使
,使![]() 的面积最大,求出点
的面积最大,求出点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水品质的需求越来越高,某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A,B两种型号的净水器共50台进行试销,其中A型净水器为x台,购买资金不超过9.8万元,试销时A型净水器每台售价2500元,B型净水器每台售价2180元,公司决定从销售A型净水器的利润中按每台捐献a元作为公司帮扶贫困村饮水改造资金.若公司售完50台净水器并捐献扶贫资金后获得的最大利润不低于20200元但不超过23000元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
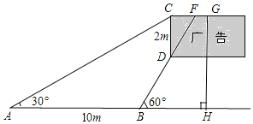
【题目】数学兴趣小组向利用所学的知识了解某广告牌的高度,已知CD=2m,经测量,得到其它数据如图所示,其中∠CAH=30°,∠DBH=60°,AB=10m,请你根据以上数据计算GH的长(要求计算结果保留根号,不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
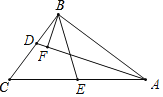
【题目】如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为( )
A.19°B.33°C.34°D.43°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com