
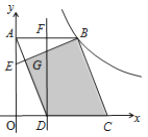
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,平行四边形
为坐标原点,平行四边形![]() 的边
的边![]() 在
在![]() 轴正半轴上,顶点
轴正半轴上,顶点![]() 在
在![]() 轴正半轴上,函数
轴正半轴上,函数![]() 的图像经过点
的图像经过点![]() ,点
,点![]() 是线段
是线段![]() 上接近点
上接近点![]() 的三等分点,
的三等分点,![]() ,垂足为点
,垂足为点![]() ,且
,且![]() 恰好是线段
恰好是线段![]() 的中点,连结
的中点,连结![]() ,
,![]() 交于点
交于点![]() ,则四边形
,则四边形![]() 的面积是()
的面积是()
A.![]() B.5C.
B.5C.![]() D.
D.![]()
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
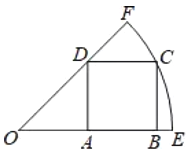
【题目】如图,正方形ABCD的四个顶点分别在扇形OEF的半径OE、OF和弧EF上,且点A是线段OB的中点,若弧EF的长为![]() π,则OD长为______________
π,则OD长为______________
查看答案和解析>>
科目:初中数学 来源: 题型:
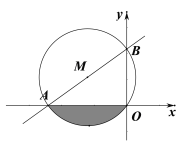
【题目】一次函数![]() 的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且
的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且![]() △OAB的外接圆的圆心M的横坐标为-3.
△OAB的外接圆的圆心M的横坐标为-3.
(1)求一次函数的解析式;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料![]() ,乙种原料
,乙种原料![]() ,现用两种原料生产处
,现用两种原料生产处![]() 两种产品共
两种产品共![]() 件,已知生产每件
件,已知生产每件![]() 产品需甲种原料
产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获得
产品可获得![]() 元;生产每件
元;生产每件![]() 产品甲种原料
产品甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获利润
产品可获利润![]() 元,设生产
元,设生产![]() 产品
产品![]() 件(产品件数为整数件),根据以上信息解答下列问题:
件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产![]() 两种产品的方案有哪几种?
两种产品的方案有哪几种?
(2)设生产这![]() 件产品可获利
件产品可获利![]() 元,写出关于
元,写出关于![]() 的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为测量底面为圆形的古塔的高度,小红和小明应用不同方法对其展开了研究,以下是他们各自的研究方法和研究数据:
小红:如图1,测角仪![]() ,
,![]() 的高度均为
的高度均为![]() ,分别测得古塔顶端的仰角为
,分别测得古塔顶端的仰角为![]() ,
,![]() ,测角仪底端的距离
,测角仪底端的距离![]() 为
为![]() .
.
小明:如图2,测角仪![]() 的高度为
的高度为![]() ,测得古塔顶端的仰角为
,测得古塔顶端的仰角为![]() ,测角仪所在位置与古塔底部边缘的最短距离
,测角仪所在位置与古塔底部边缘的最短距离![]() 为
为![]() .(参考数据:
.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )小明利用测得的数据计算古塔高度
)小明利用测得的数据计算古塔高度![]() .
.
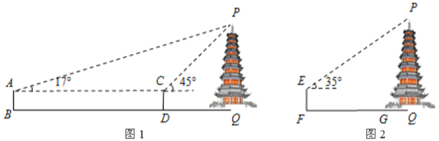
问题1:指出小明计算过程中的错误之处;
问题2:利用两人的测量数据,求出古塔底面圆的半径![]() (结果精确到
(结果精确到![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①F为CD的中点;②3AM=2DE;③tan∠EAF=![]() ;④
;④![]() ;⑤△PMN∽△DPE,正确的结论个数是( )
;⑤△PMN∽△DPE,正确的结论个数是( )
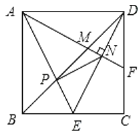
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解九年级学生的身体素质测试情况,随机抽取了该市九年级部分学生的身体素质测试成绩作为样本,按![]() (优秀),
(优秀),![]() (良好),
(良好),![]() (合格),
(合格),![]() (不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:

(1)此次共调查了多少名学生?
(2)将条形统计图补充完整,并计算扇形统计图中“![]() ”部分所对应的圆心角的度数.
”部分所对应的圆心角的度数.
(3)该市九年级共有9000名学生参加了身体素质测试,估计测试成绩在良好以上(含良好)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水品质的需求越来越高,某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A,B两种型号的净水器共50台进行试销,其中A型净水器为x台,购买资金不超过9.8万元,试销时A型净水器每台售价2500元,B型净水器每台售价2180元,公司决定从销售A型净水器的利润中按每台捐献a元作为公司帮扶贫困村饮水改造资金.若公司售完50台净水器并捐献扶贫资金后获得的最大利润不低于20200元但不超过23000元,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com