练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

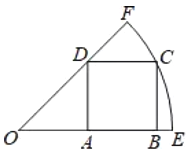
    【题目】如图，正方形ABCD的四个顶点分别在扇形OEF的半径OE、OF和弧EF上，且点A是线段OB的中点，若弧EF的长为π，则OD长为______________

    【答案】

    【解析】

    根据正方形的性质且点A是线段OB的中点得到OA=AD，得到∠AOD=45°，根据弧EF的长为π，求出半径OE，连接OC，利用勾股定理求出OA，再利用勾股定理即可得到OD.

    在正方形ABCD中，AB=AD，∠DAB=∠ABC=90°，

    ∴∠OAD=90°，

    ∵点A是线段OB的中点，

    ∴OA=AB=AD，

    ∴∠AOD=45°，

    ∵弧EF的长为π，

    ∴,

    ∴OE=，

    连接OC，则OC= OE=，

    设OA=x，则OB=2x，BC=x，

    ∴，

    解得x=4，

    ∴OD==,

    故答案为：.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校计划一次性购买排球和篮球，每个篮球的价格比排球贵30元；购买2个排球和3个篮球共需340元．

    (1)求每个排球和篮球的价格：

    (2)若该校一次性购买排球和篮球共60个，总费用不超过3800元，且购买排球的个数少于39个．设排球的个数为m，总费用为y元．

    ①求y关于m的函数关系式，并求m可取的所有值；

    ②在学校按怎样的方案购买时，费用最低？最低费用为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】綦江区某中学的国旗护卫队需从甲、乙两队中选择一队身高比较整齐的队员担任护旗手，每队中每个队员的身高（单位：cm）如下:

    甲队

    178

    177

    179

    179

    178

    178

    177

    178

    177

    179

    乙队：

    分析数据：两组样本数据的平均数、中位数、众数、方差如下表所示：

    整理、描述数据:

    平均数

    中位数

    众数

    方差

    甲队

    178

    178

    b

    0.6

    乙队

    178

    a

    178

    c

    （1）表中a=______，b=______，c=______；

    （2）根据表格中的数据，你认为选择哪个队比较好？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】平移抛物线得到抛物线，使得抛物线的顶点关于原点对称的点仍在抛物线上，下列的平移中，不能得到满足条件的抛物线的是（ ）

    A.向右平移1个单位，再向下平移2个单位

    B.向左平移1个单位，再向下平移2个单位

    C.向左平移个单位，再向下平移个单位

    D.向左平移3个单位，再向下平移9个单位

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，为的内接三角形，过点作的切线，交的延长线于，且．

    （1）求证：

    （2）若，，求的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

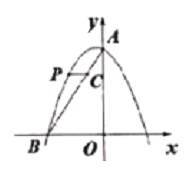
    【题目】如图，二次函数y=-x2+(n-1)x+3的图像与y轴交于点A，与x轴的负半轴交于点B(-2，0)

    (1)求二次函数的解析式；

    (2)点P是这个二次函数图像在第二象限内的一线，过点P作y轴的垂线与线段AB交于点C，求线段PC长度的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，反比例函数的图象经过点，直线与双曲线在第二四象限分别相交于两点，与轴、轴分别相交于两点连接，当时，的值是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

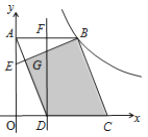
    【题目】如图，在平面直角坐标系中，为坐标原点，平行四边形的边在轴正半轴上，顶点在轴正半轴上，函数的图像经过点，点是线段上接近点的三等分点，，垂足为点，且恰好是线段的中点，连结，交于点，则四边形的面积是（）

    A.B.5C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与实践

    正方形内“奇妙点”及性质探究

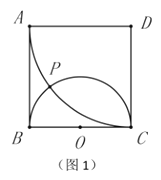
    定义：如图1，在正方形中，以为直径作半圆，以为圆心，为半径作，与半圆交于点.我们称点为正方形的一个“奇妙点”．过奇妙点的多条线段与正方形无论是位置关系还是数量关系，都具有不少优美的性质值得探究．

    性质探究：如图2，连接并延长交于点，则为半圆的切线．

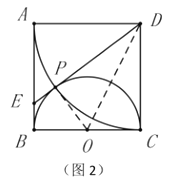
    证明：连接．

    由作图可知，，

    又．

    ，∴是半圆的切线．

    问题解决：

    （1）如图3，在图2的基础上，连接.请判断和的数量关系，并说明理由；

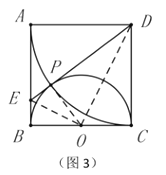
    （2）在（1）的条件下，请直接写出线段之间的数量关系；

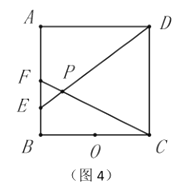
    （3）如图4，已知点为正方形的一个“奇妙点”，点为的中点，连接并延长交于点，连接并延长交于点，请写出和的数量关系，并说明理由；

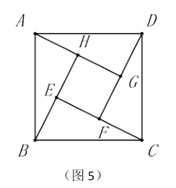
    （4）如图5，已知点为正方形的四个“奇妙点”．连接，恰好得到一个特殊的“赵爽弦图”．请根据图形，探究并直接写出一个不全等的几何图形面积之间的数量关系．

    查看答案和解析>>

    同步练习册答案