
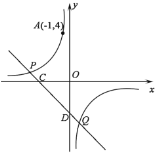
【题目】如图,反比例函数![]() 的图象经过点
的图象经过点![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 在第二四象限分别相交于
在第二四象限分别相交于![]() 两点,与
两点,与![]() 轴、
轴、![]() 轴分别相交于
轴分别相交于![]() 两点连接
两点连接![]() ,当
,当![]() 时,
时,![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据反比例函数的图象上点的坐标特征易得k=-4,然后表示出C(b,0),根据三角形面积公式,由于S△ODQ=S△OCD,所以点Q和点C到OD的距离相等,则Q的横坐标为-b,利用直线解析式可得到Q(-b,2b),再根据反比例函数的图象上点的坐标特征得到-b2b=-4,然后解方程即可得到满足条件的b的值.
解:∵反比例函数y=![]() 的图象经过点A(-1,4)
的图象经过点A(-1,4)
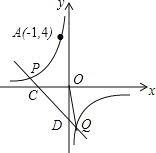
∴k=-1×4=-4;
当y=0时,-x+b=0,解得x=b,则C(b,0),
∵S△ODQ=S△OCD,
∴点Q和点C到OD的距离相等,
而Q点在第四象限,
∴Q的横坐标为-b,
当x=-b时,y=-x+b=2b,则Q(-b,2b),
∵点Q在反比例函数y=![]() 的图象上,
的图象上,
∴-b2b=-4,解得b=-![]() 或b=
或b=![]() (舍去),
(舍去),
∴b的值为-![]() .
.
故选:B


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,关于此函数的图象及性质,下列结论中不一定成立的是( )
,关于此函数的图象及性质,下列结论中不一定成立的是( )
A.该图象的顶点坐标为![]() B.该图象与
B.该图象与![]() 轴的交点为
轴的交点为![]()
C.若该图象经过点![]() ,则一定经过点
,则一定经过点![]() D.当
D.当![]() 时,
时,![]() 随
随![]() 的增大而增大
的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“扬州漆器”名扬天下,某网店专门销售某种品牌的漆器笔筒,成本为30元/件,每天销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间存在一次函数关系,如图所示.
(元)之间存在一次函数关系,如图所示.

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)如果规定每天漆器笔筒的销售量不低于240件,当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)该网店店主热心公益事业,决定从每天的销售利润中捐出150元给希望工程,为了保证捐款后每天剩余利润不低于3600元,试确定该漆器笔筒销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的四个顶点分别在扇形OEF的半径OE、OF和弧EF上,且点A是线段OB的中点,若弧EF的长为![]() π,则OD长为______________
π,则OD长为______________
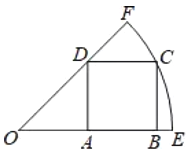
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织学生参加交通安全知识网络测试活动.小华对九年(8)班全体学生的测试成绩进行了统计,并将成绩分为四个等级:优秀、良好、一般、不合格,绘制成如下的统计图(不完整),请你根据图中所给的信息解答下列问题:
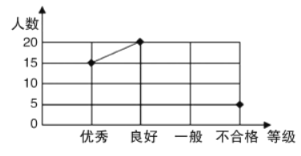
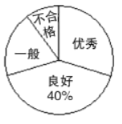
(1)九年(8)班有______名学生,并把折线统计图补充完整;
(2)已知该市共有![]() 名中学生参加了这次交通安全知识测试,请你根据该班成绩估计该市在这次测试中成绩为优秀的人数;
名中学生参加了这次交通安全知识测试,请你根据该班成绩估计该市在这次测试中成绩为优秀的人数;
(3)小华查了该市教育网站发现,全市参加本次测试的学生中,成绩为优秀的有![]() 人,请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
人,请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且
的图像与x轴的负半轴相交于点A,与y轴的正半轴相交于点B,且![]() △OAB的外接圆的圆心M的横坐标为-3.
△OAB的外接圆的圆心M的横坐标为-3.
(1)求一次函数的解析式;
(2)求图中阴影部分的面积.
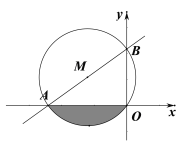
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料![]() ,乙种原料
,乙种原料![]() ,现用两种原料生产处
,现用两种原料生产处![]() 两种产品共
两种产品共![]() 件,已知生产每件
件,已知生产每件![]() 产品需甲种原料
产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获得
产品可获得![]() 元;生产每件
元;生产每件![]() 产品甲种原料
产品甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获利润
产品可获利润![]() 元,设生产
元,设生产![]() 产品
产品![]() 件(产品件数为整数件),根据以上信息解答下列问题:
件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产![]() 两种产品的方案有哪几种?
两种产品的方案有哪几种?
(2)设生产这![]() 件产品可获利
件产品可获利![]() 元,写出关于
元,写出关于![]() 的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①F为CD的中点;②3AM=2DE;③tan∠EAF=![]() ;④
;④![]() ;⑤△PMN∽△DPE,正确的结论个数是( )
;⑤△PMN∽△DPE,正确的结论个数是( )
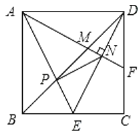
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com