
����Ŀ���ۺ���ʵ��
�����������������������̽��
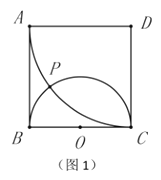
���壺��ͼ1����������![]() �У���
�У���![]() Ϊֱ������Բ
Ϊֱ������Բ![]() ����
����![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶��
Ϊ�뾶��![]() �����Բ
�����Բ![]() ���ڵ�
���ڵ�![]() .���dzƵ�
.���dzƵ�![]() Ϊ������
Ϊ������![]() ��һ��������������������Ķ����߶���������
��һ��������������������Ķ����߶���������![]() ������λ�ù�ϵ����������ϵ�������в�������������ֵ��̽����
������λ�ù�ϵ����������ϵ�������в�������������ֵ��̽����
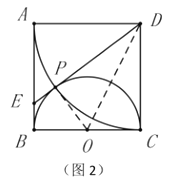
����̽������ͼ2������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ����
����![]() Ϊ��Բ
Ϊ��Բ![]() �����ߣ�
�����ߣ�
֤��������![]() ��
��
����ͼ��֪��![]() ��
��
��![]() ��
��
![]()
![]() ����
����![]() �ǰ�Բ
�ǰ�Բ![]() �����ߣ�
�����ߣ�
��������
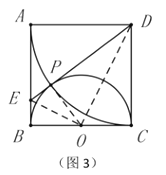
��1����ͼ3����ͼ2�Ļ����ϣ�����![]() .���ж�
.���ж�![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
��2���ڣ�1���������£���ֱ��д���߶�![]() ֮���������ϵ��
֮���������ϵ��
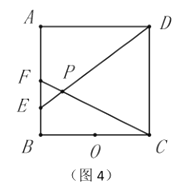
��3����ͼ4����֪��![]() Ϊ������
Ϊ������![]() ��һ���������������
��һ���������������![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ������
������![]() ���ӳ���
���ӳ���![]() �ڵ�
�ڵ�![]() ����д��
�����![]() ��
��![]() ��������ϵ����˵�����ɣ�
��������ϵ����˵�����ɣ�
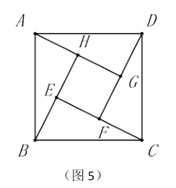
��4����ͼ5����֪��![]() Ϊ������
Ϊ������![]() ���ĸ����������������
���ĸ����������������![]() ��ǡ�õõ�һ�����������ˬ��ͼ���������ͼ�Σ�̽����ֱ��д��һ����ȫ�ȵļ���ͼ�����֮���������ϵ��
��ǡ�õõ�һ�����������ˬ��ͼ���������ͼ�Σ�̽����ֱ��д��һ����ȫ�ȵļ���ͼ�����֮���������ϵ��
���𰸡���1��![]() �����ɼ���������2��
�����ɼ���������2��![]() ����3��
����3��![]() �����ɼ���������4���𰸲�Ψһ���磺
�����ɼ���������4���𰸲�Ψһ���磺![]() ���������������
���������������![]() �������������
�������������![]() ���������������
���������������![]() �����
�����![]() �ȣ�
�ȣ�
��������
��1����������룬��ͼ2�Լ�������۵Ļ����ϣ�����ȫ�������ε����ʡ��ı��ε��ڽǺ͡��ڲ��ǵ����ʿɵó�![]() �����ɱ߱߱߶�����֤��
�����ɱ߱߱߶�����֤��![]() ��Ȼ������ȫ�������ε����ʡ���ʽ���ʿɵ�֤���ۣ�
��Ȼ������ȫ�������ε����ʡ���ʽ���ʿɵ�֤���ۣ�
��2���ɣ�1����֪![]() ��
��![]() ������ȫ�������ε����ʡ��߶εĺͲ�ɵõ����ۣ�
������ȫ�������ε����ʡ��߶εĺͲ�ɵõ����ۣ�
��3����������룬���Ӹ����߹����ֱ�������Σ��ɣ�1����֪![]() ����������ֵ��ȣ��ٸ��������ε����ʼ��ɵ�֤���ۣ�
����������ֵ��ȣ��ٸ��������ε����ʼ��ɵ�֤���ۣ�
��4������ǰ��Ľ��۽����ˬ��ͼ��֤��
![]() ������������룮
������������룮
�⣺��1�����ۣ�![]()
�������£�
��![]()
��![]() ��
��![]() ��
��![]()
��![]()
��![]()
��![]()
��![]() ��
��![]() ��
��
��![]() ��
��![]()
��![]()
��![]()
��![]()
��![]() ��
��
��2�����ɣ�1����֪��![]() ��
��![]()
��![]() ��
��![]()
��![]()
��![]()
���߶�![]() ��
��![]() ��
��![]() ֮���������ϵ��
֮���������ϵ��![]() ��
��
��3�����ۣ�![]()
���ɣ�����![]() ��
��![]() ����ͼ��
����ͼ��
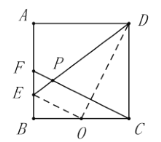
�ɣ�1����֪��![]()
��![]()
��![]()
�ߵ�![]() Ϊ
Ϊ![]() ���е�
���е�
��![]()
��![]()
���ı���![]() ��������
��������
��![]()
��![]() ��
��
��4���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ����ͼ��
����ͼ��
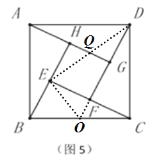
����ǰ��Ľ��ۿ�֪![]()
��![]()
�ߴ�ͼΪ��ˬ��ͼ��![]()
��![]()
ͬ���ɵ�![]() ��
��![]() ��
��![]()
���ı���![]() ��������
��������
��![]()
��![]()
����![]() ��
��![]() ��
�У�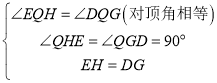
��![]()
��![]()
��![]()
��![]()
��𰸲�Ψһ�����磬![]() ���������������
���������������![]() �������������
�������������![]() ���������������
���������������![]() �����
�����![]() �ȵȣ�
�ȵȣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
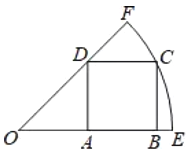
����Ŀ����ͼ��������ABCD���ĸ�����ֱ�������OEF�İ뾶OE��OF�ͻ�EF�ϣ��ҵ�A���߶�OB���е㣬����EF�ij�Ϊ![]() ������OD��Ϊ______________
������OD��Ϊ______________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
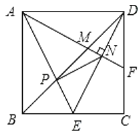
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2����E��BC���е㣬AE��BD���ڵ�P��F��CD��һ�㣬����AF�ֱ�BD��DE�ڵ�M��N����AF��DE������PN�������½����У���FΪCD���е㣻��3AM=2DE����tan��EAF��![]() ����
����![]() ���ݡ�PMN�ס�DPE����ȷ�Ľ��۸����ǣ� ��
���ݡ�PMN�ס�DPE����ȷ�Ľ��۸����ǣ� ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽���꼶ѧ�����������ʲ�������������ȡ�˸��о��꼶����ѧ�����������ʲ��Գɼ���Ϊ��������![]() �����㣩��
�����㣩��![]() �����ã���
�����ã���![]() ���ϸ�
���ϸ�![]() �����ϸ��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ������������������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺
�����ϸ��ĸ��ȼ�����ͳ�ƣ�����ͳ�ƽ������������������������ͳ��ͼ�������ͼ���ṩ����Ϣ������������⣺

��1���˴ι������˶�����ѧ����
��2��������ͳ��ͼ��������������������ͳ��ͼ����![]() ����������Ӧ��Բ�ĽǵĶ�����
����������Ӧ��Բ�ĽǵĶ�����
��3�����о��꼶����9000��ѧ���μ����������ʲ��ԣ����Ʋ��Գɼ����������ϣ������ã���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����y��mx2����2m+1��x+2��m��0�������ж����н����Ƿ���ȷ����˵�����ɣ�
��1����m��0ʱ������y��mx2����2m+1��x+2��x��1ʱ��y��x���������С��
��2����m��0ʱ������y��mx2����2m+1��x+2ͼ���x���ϵ��߶γ���С��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
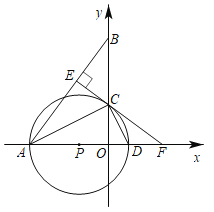
����Ŀ����ͼ����AOB�У�A��-8��0����B��0��![]() ����ACƽ�֡�OAB����y���ڵ�C����P��x����һ�㣬��P������A��C����x�ύ�ڵ�D������C��CE��AB������ΪE��EC���ӳ��߽�x���ڵ�F��
����ACƽ�֡�OAB����y���ڵ�C����P��x����һ�㣬��P������A��C����x�ύ�ڵ�D������C��CE��AB������ΪE��EC���ӳ��߽�x���ڵ�F��
��1����֤��EFΪ��P�����ߣ�
��2�����P�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����AOB��ͼ����1��������OA��ȡһ��C���Ե�OΪԲ�ģ�OC��Ϊ�뾶��![]() ��������OB�ڵ�D������CD��
��������OB�ڵ�D������CD��
��2���ֱ��Ե�C��DΪԲ�ģ�CD��Ϊ�뾶��������![]() �ڵ�M��N��
�ڵ�M��N��
��3������OM��MN��
����������ͼ���̼�����ͼ�Σ����н����д�����ǣ� ��

A. ��COM=��CODB. ��OM=MN������AOB=20��
C. MN��CDD. MN=3CD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ˮƽ����ߣ����Ƕ���ˮƷ�ʵ�����Խ��Խ�ߣ�ij��˾�����г��������A��B�����ͺŵľ�ˮ����ÿ̨A�;�ˮ����ÿ̨B�;�ˮ�����۶�200Ԫ����5��Ԫ����A�;�ˮ������4.5��Ԫ����B�;�ˮ�����������
��1����ÿ̨A�͡�B�;�ˮ���Ľ��۸��Ƕ���Ԫ��
��2���ù�˾�ƻ�����A��B�����ͺŵľ�ˮ����50̨��������������A�;�ˮ��Ϊx̨�������ʽ���9.8��Ԫ������ʱA�;�ˮ��ÿ̨�ۼ�2500Ԫ��B�;�ˮ��ÿ̨�ۼ�2180Ԫ����˾����������A�;�ˮ���������а�ÿ̨����aԪ��Ϊ��˾���ƶ������ˮ�����ʽ�����˾����50̨��ˮ��������ƶ�ʽ���õ����������20200Ԫ��������23000Ԫ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����y��2x��y����x��ͼ��ֱ�Ϊֱ��l1��l2�����㣨1��0����x��Ĵ��߽�l1�ڵ�A1������A1��y��Ĵ��߽�l2�ڵ�A2������A2��x��Ĵ��߽�l1�ڵ�A3������A3��y��Ĵ��߽�l2�ڵ�A4���������ν�����ȥ�����A2019������Ϊ��������
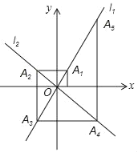
A.��21009��21010��B.����21009��21010��
C.��21009����21010��D.����21009����21010��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com