
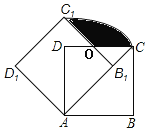
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则图中阴影部分的面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】某工厂有甲种原料![]() ,乙种原料
,乙种原料![]() ,现用两种原料生产处
,现用两种原料生产处![]() 两种产品共
两种产品共![]() 件,已知生产每件
件,已知生产每件![]() 产品需甲种原料
产品需甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获得
产品可获得![]() 元;生产每件
元;生产每件![]() 产品甲种原料
产品甲种原料![]() ,乙种原料
,乙种原料![]() ,且每件
,且每件![]() 产品可获利润
产品可获利润![]() 元,设生产
元,设生产![]() 产品
产品![]() 件(产品件数为整数件),根据以上信息解答下列问题:
件(产品件数为整数件),根据以上信息解答下列问题:
(1)生产![]() 两种产品的方案有哪几种?
两种产品的方案有哪几种?
(2)设生产这![]() 件产品可获利
件产品可获利![]() 元,写出关于
元,写出关于![]() 的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
的函数解析式,写出(1)中利润最大的方案,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2﹣(2m+1)x+2(m≠0),请判断下列结论是否正确,并说明理由.
(1)当m<0时,函数y=mx2﹣(2m+1)x+2在x>1时,y随x的增大而减小;
(2)当m>0时,函数y=mx2﹣(2m+1)x+2图象截x轴上的线段长度小于2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() .将
.将![]() 绕点
绕点![]() 逆时针方向旋转,记旋转角为
逆时针方向旋转,记旋转角为![]() .
.
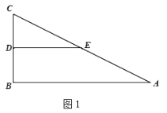

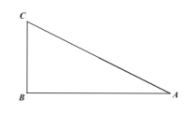
(1)问题发现
①当![]() 时,
时,![]() ____________;②当
____________;②当![]() 时,
时,![]() ___________.
___________.
(2)拓展探究试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
(3)问题解决
![]() 绕点
绕点![]() 逆时针旋转至
逆时针旋转至![]() 三点在同一条直线上时,直接写出线段
三点在同一条直线上时,直接写出线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水品质的需求越来越高,某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A,B两种型号的净水器共50台进行试销,其中A型净水器为x台,购买资金不超过9.8万元,试销时A型净水器每台售价2500元,B型净水器每台售价2180元,公司决定从销售A型净水器的利润中按每台捐献a元作为公司帮扶贫困村饮水改造资金.若公司售完50台净水器并捐献扶贫资金后获得的最大利润不低于20200元但不超过23000元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 的直线与矩形
的直线与矩形![]() 的边
的边![]() 交于点
交于点![]() ,且点
,且点![]() 不与点
不与点![]() 重合.以
重合.以![]() 为一边作菱形
为一边作菱形![]() ,点
,点![]() 在矩形
在矩形![]() 的边
的边![]() 上,设直线
上,设直线![]() 的函数表达式为
的函数表达式为![]() .
.
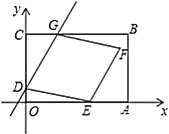
(1)当![]() 时,求直线
时,求直线![]() 的函数表达式;
的函数表达式;
(2)当点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 的函数表达式;
的函数表达式;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的长为
的长为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数表达式及自变量
的函数表达式及自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=
的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=![]() 的点P的个数是( )
的点P的个数是( )

A.0B.4C.8D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
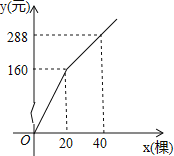
【题目】为更新树木品种,某植物园计划购进甲、乙两个品种的树苗栽植培育若计划购进这两种树苗共41棵,其中甲种树苗的单价为6元/棵,购买乙种树苗所需费用y(元)与购买数量x(棵)之间的函数关系如图所示.
(1)求出y与x的函数关系式;
(2)若在购买计划中,乙种树苗的数量不超过35棵,但不少于甲种树苗的数量.请设计购买方案,使总费用最低,并求出最低费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com