
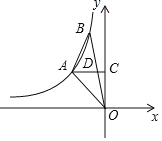
【题目】如图,A、B是反比例函数![]() 图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
图象上的两点,过点A作AC⊥y轴,垂足为C,交OB于点D,且D为OB的中点,若△ABO的面积为4,则k的值为______.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E是BC的中点,AE与BD交于点P,F是CD上一点,连接AF分别交BD,DE于点M,N,且AF⊥DE,连接PN,则以下结论中:①F为CD的中点;②3AM=2DE;③tan∠EAF=![]() ;④
;④![]() ;⑤△PMN∽△DPE,正确的结论个数是( )
;⑤△PMN∽△DPE,正确的结论个数是( )
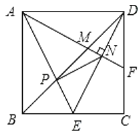
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作![]() ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;
(2)分别以点C,D为圆心,CD长为半径作弧,交![]() 于点M,N;
于点M,N;
(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水品质的需求越来越高,某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A,B两种型号的净水器共50台进行试销,其中A型净水器为x台,购买资金不超过9.8万元,试销时A型净水器每台售价2500元,B型净水器每台售价2180元,公司决定从销售A型净水器的利润中按每台捐献a元作为公司帮扶贫困村饮水改造资金.若公司售完50台净水器并捐献扶贫资金后获得的最大利润不低于20200元但不超过23000元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
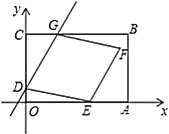
【题目】如图,平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 的坐标为
的坐标为![]() ,顶点
,顶点![]() ,
,![]() 分别在
分别在![]() 轴,
轴,![]() 轴上,点
轴上,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 的直线与矩形
的直线与矩形![]() 的边
的边![]() 交于点
交于点![]() ,且点
,且点![]() 不与点
不与点![]() 重合.以
重合.以![]() 为一边作菱形
为一边作菱形![]() ,点
,点![]() 在矩形
在矩形![]() 的边
的边![]() 上,设直线
上,设直线![]() 的函数表达式为
的函数表达式为![]() .
.
(1)当![]() 时,求直线
时,求直线![]() 的函数表达式;
的函数表达式;
(2)当点![]() 的坐标为
的坐标为![]() 时,求直线
时,求直线![]() 的函数表达式;
的函数表达式;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的长为
的长为![]() ,请直接写出
,请直接写出![]() 与
与![]() 的函数表达式及自变量
的函数表达式及自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
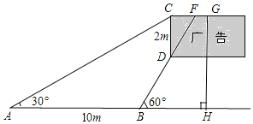
【题目】数学兴趣小组向利用所学的知识了解某广告牌的高度,已知CD=2m,经测量,得到其它数据如图所示,其中∠CAH=30°,∠DBH=60°,AB=10m,请你根据以上数据计算GH的长(要求计算结果保留根号,不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=
的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=![]() 的点P的个数是( )
的点P的个数是( )

A.0B.4C.8D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…,依次进行下去,则点A2019的坐标为( )
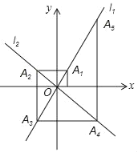
A.(21009,21010)B.(﹣21009,21010)
C.(21009,﹣21010)D.(﹣21009,﹣21010)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙、丁从笔试、面试两个方面进行量化考核.甲、乙、丙、丁两项得分如下表:(单位:分)
甲 | 乙 | 丙 | 丁 | |
笔试 | 86 | 92 | 80 | 90 |
面试 | 90 | 88 | 94 | 84 |
(1)这4名选手笔试成绩的中位数是 分,面试的平均数是 分.
(2)该公司规定:笔试、面试分别按40%,60%的比例计入总分,且各项成绩都不得低于85分. 根据规定,请你说明谁将被录用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com