
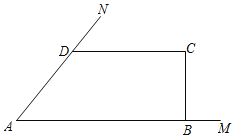
【题目】某市政府为了扶贫,鼓励当地农民养殖小龙虾,如图:张叔叔顺着圩梗AN、AM(AN=3![]() m,AM=10m,∠MAN=45°),用8m长的渔网搭建了一个养殖水域(即四边形ABCD),圩梗边不需要渔网,AB∥CD,∠C=90°.设BC=xm,四边形ABCD面积为S(m2).
m,AM=10m,∠MAN=45°),用8m长的渔网搭建了一个养殖水域(即四边形ABCD),圩梗边不需要渔网,AB∥CD,∠C=90°.设BC=xm,四边形ABCD面积为S(m2).
(1)求出S关于x的函数表达式及x的取值范围;
(2)x为何值时,围成的养殖水域面积最大?最大面积是多少?
【答案】(1)S=﹣![]() x2+8x,0<x≤3;(2)当x=3时时,围成的养殖水域面积最大,最大面积是
x2+8x,0<x≤3;(2)当x=3时时,围成的养殖水域面积最大,最大面积是![]()
![]() .
.
【解析】
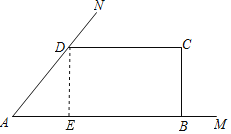
(1)过D作DE⊥AB于E,根据矩形的性质得到DE=x,求得AE=x,根据三角形和矩形的面积公式即可得到结论;
(2)根据二次函数的性质,即可得到结论.
(1)过D作DE⊥AB于E,
∵BC=xm,
∴DE=xm,
∵∠A=45°,
∴AE=xm,
∴S=S△AED+S矩形DEBC=![]() x2+(8﹣x)x=﹣
x2+(8﹣x)x=﹣![]() x2+8x,
x2+8x,
∵AB=AE+EB=x+(8﹣x)=8m,
∴B点为定点,
∴DE最大为3m,
∴0<x≤3;
(2)∵S=﹣![]() x2+8x=﹣
x2+8x=﹣![]() (x﹣8)2+32,
(x﹣8)2+32,
∴当x<8时,S随x的增大而增大,
∵0<x≤3,
∴当x=3时,S取得最大值,S最大=﹣![]() ×(3﹣8)2+32=
×(3﹣8)2+32=![]() ,
,
答:当x=3m时,围成的养殖水域面积最大,最大面积是![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】某市为了解九年级学生的身体素质测试情况,随机抽取了该市九年级部分学生的身体素质测试成绩作为样本,按![]() (优秀),
(优秀),![]() (良好),
(良好),![]() (合格),
(合格),![]() (不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
(不合格)四个等级进行统计,并将统计结果绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:

(1)此次共调查了多少名学生?
(2)将条形统计图补充完整,并计算扇形统计图中“![]() ”部分所对应的圆心角的度数.
”部分所对应的圆心角的度数.
(3)该市九年级共有9000名学生参加了身体素质测试,估计测试成绩在良好以上(含良好)的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活水平的提高,人们对饮水品质的需求越来越高,某公司根据市场需求代理A,B两种型号的净水器,每台A型净水器比每台B型净水器进价多200元,用5万元购进A型净水器与用4.5万元购进B型净水器的数量相等
(1)求每台A型、B型净水器的进价各是多少元?
(2)该公司计划购进A,B两种型号的净水器共50台进行试销,其中A型净水器为x台,购买资金不超过9.8万元,试销时A型净水器每台售价2500元,B型净水器每台售价2180元,公司决定从销售A型净水器的利润中按每台捐献a元作为公司帮扶贫困村饮水改造资金.若公司售完50台净水器并捐献扶贫资金后获得的最大利润不低于20200元但不超过23000元,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
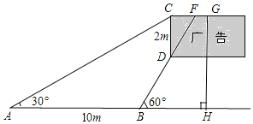
【题目】数学兴趣小组向利用所学的知识了解某广告牌的高度,已知CD=2m,经测量,得到其它数据如图所示,其中∠CAH=30°,∠DBH=60°,AB=10m,请你根据以上数据计算GH的长(要求计算结果保留根号,不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=
的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=![]() 的点P的个数是( )
的点P的个数是( )

A.0B.4C.8D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
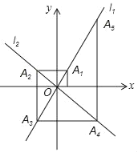
【题目】如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…,依次进行下去,则点A2019的坐标为( )
A.(21009,21010)B.(﹣21009,21010)
C.(21009,﹣21010)D.(﹣21009,﹣21010)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,∠C=52°,BE为AC边上的中线,AD平分∠BAC,交BC边于点D,过点B作BF⊥AD,垂足为F,则∠EBF的度数为( )
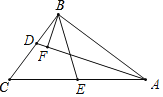
A.19°B.33°C.34°D.43°
查看答案和解析>>
科目:初中数学 来源: 题型:
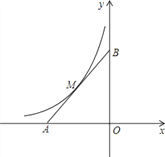
【题目】已知,在平面直角坐标系xOy中,点A在x轴负半轴上,点B在y轴正半轴上,OA=OB,函数![]() 的图象与线段AB交于M点,且AM=BM.
的图象与线段AB交于M点,且AM=BM.
(1)求点M的坐标;
(2)求直线AB的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com