
【题目】在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3,![]() ),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.
),点C的坐标为(1,0),点P为斜边OB上的一动点,则PA+PC的最小值_____.

【答案】![]()
【解析】
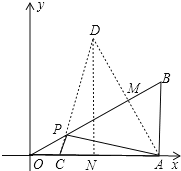
作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,则此时PA+PC的值最小,求出AM,求出AD,求出DN、CN,根据勾股定理求出CD,即可得出答案.
解:作A关于OB的对称点D,连接CD交OB于P,连接AP,过D作DN⊥OA于N,
则此时PA+PC的值最小,
∵DP=PA,
∴PA+PC=PD+PC=CD,
∵B(3,![]() ),
),
∴AB=![]() ,OA=3,∠B=60°,由勾股定理得:OB=
,OA=3,∠B=60°,由勾股定理得:OB=![]() ,
,
由三角形面积公式得:![]() ×OA×AB=
×OA×AB=![]() ×OB×AM,
×OB×AM,
∴AM=![]() ,
,
∴AD=2×![]() =3,
=3,
∵∠AMB=90°,∠B=60°,
∴∠BAM=30°,
∵∠BAO=90°,
∴∠OAM=60°,
∵DN⊥OA,
∴∠NDA=30°,
∴AN=![]() AD=
AD=![]() ,由勾股定理得:DN=
,由勾股定理得:DN=![]() ,
,
∵C(1,0),
∴CN=3-1-![]() =
=![]() ,
,
在Rt△DNC中,由勾股定理得:DC=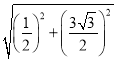 =
=![]() ,
,
即PA+PC的最小值是![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】庆元大道两侧需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
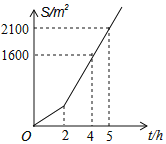
A. 200B. 300C. 400D. 500
查看答案和解析>>
科目:初中数学 来源: 题型:
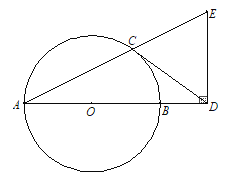
【题目】如图,AB是⊙O的直径,CD与⊙O相切于点C,与AB的延长线交于点D,DE⊥AD且与AC的延长线交于点E.
(1)求证:DC=DE;
(2)若tan∠CAB=![]() ,AB=3,求BD的长.
,AB=3,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
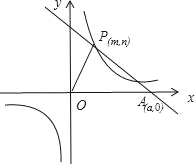
【题目】已知:O是坐标原点,P(m,n)(m>0)是函数y=![]() (k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+
(k>0)上的点,过点P作直线PA⊥OP于P,直线PA与x轴的正半轴交于点A(a,0)(a>m).设△OPA的面积为s,且s=1+![]() .
.
(1)当n=1时,求点A的坐标;
(2)若OP=AP,求k的值;
(3)设n是小于20的整数,且k≠![]() ,求OP2的最小值.
,求OP2的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△OAB是⊙O的内接三角形,∠AOB=120°,过O作OE⊥AB于点E,交⊙O于点C,延长OB至点D,使OB=BD,连CD.
(1)求证: CD是⊙O切线;
(2)若F为OE上一点,BF的延长线交⊙O于G,连OG,![]() ,CD=6
,CD=6![]() ,求S△GOB.
,求S△GOB.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB=12cm,点C在线段AB上,点D、E分别是AC和BC的中点.
(1)若点C恰好是AB中点,求DE的长.
(2)若AC=4cm,求DE的长.
(3)若点C为线段AB上的一个动点(点C不与A,B重合),求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将若干枝铅笔分给甲、乙两个班级,甲班有一人分到6枝,其余的每人都分到13枝,乙班有一人分到5枝,其余的每人都分到10枝.如果分到两个班级的铅笔数目相同,并且大于100而不超过200那么甲、乙两个班各有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com