
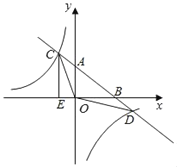
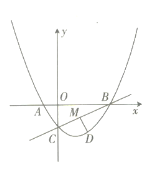
【题目】如图,一次函数y=ax+b的图象与反比例函数y=![]() 的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=
的图象交于C,D两点,与x,y轴交于B,A两点,CE⊥x轴于点E,且tan∠ABO=![]() ,OB=4,OE=1.
,OB=4,OE=1.
(1)求一次函数的解析式和反比例函数的解析式
(2)求△OCD的面积;
(3)根据图象直接写出一次函数的值大于反比例函数的值时,自变量x的取值范围.
【答案】(1) y=﹣![]() x+2, y=﹣
x+2, y=﹣![]() ;(2) 6;(3) x<﹣1或0<x<5
;(2) 6;(3) x<﹣1或0<x<5
【解析】
(1)根据tan∠ABO=![]() ,OB=4,OE=1先把A、B、C点的坐标算出来,再用待定系数法即可把一次函数的解析式和反比例函数的解析式计算出来;
,OB=4,OE=1先把A、B、C点的坐标算出来,再用待定系数法即可把一次函数的解析式和反比例函数的解析式计算出来;
(2) 联立反比例函数的解析式和直线AB的解析式可得这两个函数图像的交点坐标,再根据面积公式即可求解;
(3)根据函数图像可以直接写出结果.
(1)∵OB=4,OE=1,
∴BE=1+4=5.
∵CE⊥x轴于点E,tan∠ABO=![]() =
=![]() =
=![]() ,
,
∴OA=2,CE=2.5.
∴点A的坐标为(0,2)、点B的坐标为C(4,0)、点C的坐标为(﹣1,2.5).
∵一次函数y=ax+b的图象与x,y轴交于B,A两点,
∴![]() ,
,
解得 .
.
∴直线AB的解析式为y=﹣![]() x+2.
x+2.
∵反比例函数y=![]() 的图象过C,
的图象过C,
∴2.5=![]() ,
,
∴k=﹣2.5,
∴该反比例函数的解析式为y=﹣![]() ;
;
(2)联立反比例函数的解析式和直线AB的解析式可得 ,
,
解得点D的坐标为(5,﹣![]() ),
),
则△BOD的面积=4×![]() ×
×![]() =1,
=1,
△BOC的面积=4×![]() ×
×![]() =5,
=5,
∴△OCD的面积为1+5=6;
(3)由图象和点C、D的坐标得,一次函数的值大于反比例函数的值时x的取值范围:x<﹣1或0<x<5.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点B的坐标为(4,2),直线y=﹣![]() x+
x+![]() 与边AB,BC分别相交于点M,N,函数y=
与边AB,BC分别相交于点M,N,函数y=![]() (x>0)的图象过点M.
(x>0)的图象过点M.
(1)试说明点N也在函数y=![]() (x>0)的图象上;
(x>0)的图象上;
(2)将直线MN沿y轴的负方向平移得到直线M′N′,当直线M′N′与函数y═![]() (x>0)的图象仅有一个交点时,求直线M'N′的解析式.
(x>0)的图象仅有一个交点时,求直线M'N′的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
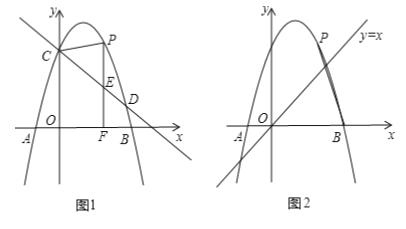
【题目】如图1,抛物线![]() 与
与![]() 轴于点
轴于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .直线
.直线![]() 经过点
经过点![]() ,与抛物线另一个交点为
,与抛物线另一个交点为![]() ,点
,点![]() 是抛物线上一动点,过点
是抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 上方,且
上方,且![]() 是以
是以![]() 为腰的等腰三角形时,求点
为腰的等腰三角形时,求点![]() 的坐标;
的坐标;
(3)如图2,连接![]() ,以点
,以点![]() 为直角顶点,线段
为直角顶点,线段![]() 为较长直角边,构造两直角边比为1:2的
为较长直角边,构造两直角边比为1:2的![]() ,是否存在点
,是否存在点![]() ,使点
,使点![]() 恰好落在直线
恰好落在直线![]() 上?若存在,请直接写出相应点
上?若存在,请直接写出相应点![]() 的横坐标(写出两个即可);若不存在,请说明理由.
的横坐标(写出两个即可);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于灯塔A的南偏西75°方向的B处,距离A处30海里,渔船沿北偏东30°方向追寻鱼群,航行一段时间后,到达位于A处北偏西20°方向的C处,渔船出现了故障立即向正在灯塔A处的巡逻船发出求救信号.巡逻船收到信号后以40海里每小时的速度前往救助,请问巡逻船多少分钟能够到达C处?(参考数据:![]() ≈1.4,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,最后结果精确到1分钟).
≈1.4,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,最后结果精确到1分钟).
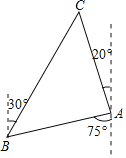
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() 二次函数
二次函数![]() 的图象经过
的图象经过![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
![]() 求二次函数的解析式及点
求二次函数的解析式及点![]() 的坐标.
的坐标.
![]() 点
点![]() 是线段
是线段![]() 上的一动点,动点
上的一动点,动点![]() 在直线
在直线![]() 下方的二次函数图象上.设点
下方的二次函数图象上.设点![]() 的横坐标为
的横坐标为![]() .过点
.过点![]() 作
作![]() 于点
于点![]() 求线段
求线段![]() 的长关于
的长关于![]() 的函数解析式,并求线段
的函数解析式,并求线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.
(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°.
①若AB=CD=1,AB∥CD,求对角线BD的长.
②若AC⊥BD,求证:AD=CD;
(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】昆明市某中学“综合实践活动”棋类社团前两次购买的两种材质的围棋采购如表(近期两种材质的围棋的售价一直不变):
塑料围棋 | 玻璃围棋 | 总价(元) | |
第一次(盒) |
|
|
|
第二次(盒) |
|
|
|
(1)若该社团计划再采购这两种材质的围棋各![]() 盒,则需要多少元;
盒,则需要多少元;
(2)若该社团准备购买这两种材质的围棋共![]() 盒,且要求塑料围棋的数量不多于玻璃围棋数量的
盒,且要求塑料围棋的数量不多于玻璃围棋数量的![]() 倍,请设计出最省钱的购买方案,并说明理由.
倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com