
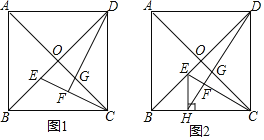
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.

【答案】(1)证明见解析;(2)①证明见解析;②HC=![]() .
.
【解析】
(1)要证明OE=OG,只要证明△DOG≌△COE(ASA)即可;
(2)①要证明∠ODG=∠OCE,只要证明△ODG≌△OCE即可;
②设CH=x,由△CHE∽△DCH,可得![]() =
=![]() ,即HC2=EHCD,由此构建方程即可解决问题;
,即HC2=EHCD,由此构建方程即可解决问题;
(1)证明:如图1中,
∵四边形ABCD是正方形,
∴AC⊥BD,OD=OC,
∴∠DOG=∠COE=90°,
∴∠OEC+∠OCE=90°,
∵DF⊥CE,
∴∠OEC+∠ODG=90°,
∴∠ODG=∠OCE,
∴△DOG≌△COE(ASA),
∴OE=OG.
(2)①证明:如图2中,
∵AC,BD为对角线,
∴OD=OC,
∵OG=OE,∠DOG=∠COE=90°,
∴△ODG≌△OCE,
∴∠ODG=∠OCE.
②解:设CH=x,
∵四边形ABCD是正方形,AB=1,
∴BH=1-x,∠DBC=∠BDC=∠ACB=45°,
∵EH⊥BC,
∴∠BEH=∠EBH=45°,
∴EH=BH=1-x,
∵∠ODG=∠OCE,
∴∠BDC-∠ODG=∠ACB-∠OCE,
∴∠HDC=∠ECH,
∵EH⊥BC,
∴∠EHC=∠HCD=90°,
∴△CHE∽△DCH,
∴![]() =
=![]() ,
,
∴HC2=EHCD,
∴x2=(1-x)1,
解得x=![]() 或
或![]() (舍弃),
(舍弃),
∴HC=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题:
①方程![]() 的解为
的解为 ![]() ;
;
②方程![]() 的解为
的解为 ![]() ,
,![]() ;
;
③方程![]() 的解为
的解为 ![]() ,
,![]() ;
;
…
(1)根据以上方程特征及其解的特征,请猜想:
①方程![]() 的解为________;
的解为________;
②关于![]() 的方程________的解为
的方程________的解为![]() ,
,![]() .
.
(2)请用配方法解方程![]() ,以验证猜想结论的正确性.
,以验证猜想结论的正确性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像为直线
的图像为直线![]() .
.
(1)若直线![]() 与正比例函数
与正比例函数![]() 的图像平行,且过点(0,2),求直线
的图像平行,且过点(0,2),求直线![]() 的函数表达式;
的函数表达式;
(2)若直线![]() 过点(3,0),且与两坐标轴围成的三角形面积等于3,求
过点(3,0),且与两坐标轴围成的三角形面积等于3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB为半圆O的直径,D为BA的延长线上一点,DC为半圆O的切线,切点为C.
(1)求证:∠ACD=∠B;
(2)如图(2),∠BDC的平分线分别交AC,BC于点E,F,求∠CEF的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需280元;购买3个A品牌和1个B品牌的计算器共需210元.
(Ⅰ)求这两种品牌计算器的单价;
(Ⅱ)开学前,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的九折销售,B品牌计算器10个以上超出部分按原价的七折销售.设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1,y2关于x的函数关系式.
(Ⅲ)某校准备集体购买同一品牌的计算器,若购买计算器的数量超过15个,购买哪种品牌的计算器更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD对角线AC上一动点,点E在射线BC上,且PB=PE,连接PD,O为AC中点.
(1)如图1,当点P在线段AO上时,试猜想PE与PD的数量关系和位置关系,不用说明理由;
(2)如图2,当点P在线段OC上时,(1)中的猜想还成立吗?请说明理由;
(3)如图3,当点P在AC的延长线上时,请你在图3中画出相应的图形(尺规作图,保留作图痕迹,不写作法),并判断(1)中的猜想是否成立?若成立,请直接写出结论;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1B2,△A2B2B3,△A3B3B4,…均为等边三角形.若OB1=1,则△A8B8B9的边长为( )
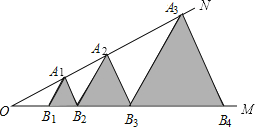
A.64B.128C.132D.256
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+(2﹣a)x﹣2(a>0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C.给出下列结论:
①在a>0的条件下,无论a取何值,点A是一个定点;
②在a>0的条件下,无论a取何值,抛物线的对称轴一定位于y轴的左侧;
③y的最小值不大于﹣2;
④若AB=AC,则a=![]() .
.
其中正确的结论有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com