
【题目】一次函数![]() 的图像为直线
的图像为直线![]() .
.
(1)若直线![]() 与正比例函数
与正比例函数![]() 的图像平行,且过点(0,2),求直线
的图像平行,且过点(0,2),求直线![]() 的函数表达式;
的函数表达式;
(2)若直线![]() 过点(3,0),且与两坐标轴围成的三角形面积等于3,求
过点(3,0),且与两坐标轴围成的三角形面积等于3,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】![]() 如图一:小明想测量一棵树的高度
如图一:小明想测量一棵树的高度![]() ,在阳光下,小明测得一根与地面垂直、长为
,在阳光下,小明测得一根与地面垂直、长为![]() 米的竹竿的影长为
米的竹竿的影长为![]() 米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长
米.同时另一名同学测量一棵树的高度时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),墙壁上的影长![]() 为
为![]() 米,落在地面上的影长
米,落在地面上的影长![]() 为
为![]() 米,则树高
米,则树高![]() 为多少米.
为多少米.
![]() 如图二:在阳光下,小明在某一时刻测得与地面垂直、长为
如图二:在阳光下,小明在某一时刻测得与地面垂直、长为![]() 的杆子在地面上的影子长为
的杆子在地面上的影子长为![]() ,在斜坡上影长为
,在斜坡上影长为![]() ,他想测量电线杆
,他想测量电线杆![]() 的高度,但其影子恰好落在土坡的坡面
的高度,但其影子恰好落在土坡的坡面![]() 和地面
和地面![]() 上,量得
上,量得![]() ,
,![]() ,求电线杆的高度.
,求电线杆的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九年级(1)班全班50名同学组成五个不同的兴趣爱好小组,每人都参加且只能参加一个小组,统计(不完全)人数如下表:
编号 | 一 | 二 | 三 | 四 | 五 |
人数 |
| 15 | 20 | 10 |
|
已知前面两个小组的人数之比是![]() .
.
解答下列问题:
(1)![]() .
.
(2)补全条形统计图:
(3)若从第一组和第五组中任选两名同学,求这两名同学是同一组的概率.(用树状图或列表把所有可能都列出来)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC、BC为边,在Rt△ABC外作两个等边三角形△ACE和△BCF,连接BE、AF分别交AC、BC边于H、D两点.下列结论:①AF=BE;②∠AFC=∠EBC;③∠FAE=90°;④BD=FD,其中正确结论的个数是( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() .
.
(1)当![]() 时;
时;
①求一次函数的表达式;
②![]() 平分
平分![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(2)若△![]() 为等腰三角形,求
为等腰三角形,求![]() 的值;
的值;
(3)若直线![]() 也经过点
也经过点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.


查看答案和解析>>
科目:初中数学 来源: 题型:
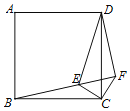
【题目】如图,在正方形ABCD内一点E连接BE、CE,过C作CF⊥CE与BE延长线交于点F,连接DF、DE.CE=CF=1,DE=![]() ,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=
,下列结论中:①△CBE≌△CDF;②BF⊥DF;③点D到CF的距离为2;④S四边形DECF=![]() +1.其中正确结论的个数是( )
+1.其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD的对角线AC,BD相交于点O.
(1)如图1,E,G分别是OB,OC上的点,CE与DG的延长线相交于点F.若DF⊥CE,求证:OE=OG;
(2)如图2,H是BC上的点,过点H作EH⊥BC,交线段OB于点E,连结DH交CE于点F,交OC于点G.若OE=OG,
①求证:∠ODG=∠OCE;
②当AB=1时,求HC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积是
A.126 cm2 或66 cm2B.66 cm2C.120 cm2D.126cm2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com