
【题目】如图,长方形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,点
,点![]() 是边
是边![]() 上一点,连接
上一点,连接![]() ,将四边形
,将四边形![]() 沿
沿![]() 折叠,若点
折叠,若点![]() 的对称点
的对称点![]() 恰好落在边
恰好落在边![]() 上,则
上,则![]() 的长为____.
的长为____.

【答案】3.
【解析】
根据矩形的性质得到BC=OA=8,OC=AB=6,∠C=∠B=∠O=90°,求得CD=6,BD=2,根据折叠可知A′D=AD,A′E=AE,可证明Rt△A′CD≌Rt△DBA,根据全等三角形的性质得到A′C=BD=2,A′O=4,然后在Rt△A′OE中根据勾股定理列出方程求解即可.
解:如图, 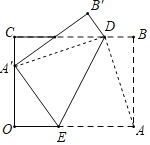
∵四边形OABC是矩形,
∴BC=OA=8,OC=AB=6,∠C=∠B=∠O=90°,
∵CD=3DB,
∴CD=6,BD=2,
∴CD=AB,
∵将四边形ABDE沿DE折叠,若点A的对称点A′恰好落在边OC上,
∴A′D=AD,A′E=AE,
在Rt△A′CD与Rt△DBA中,
![]() ,
,
∴Rt△A′CD≌Rt△DBA(HL),
∴A′C=BD=2,
∴A′O=4,
∵A′O2+OE2=A′E2,
∴42+OE2=(8-OE)2,
∴OE=3,
故答案是:3.


 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB=10,P是线段AB上的动点,分别以AP、PB为边在线段AB的同侧作等边△ACP和△PDB,连接CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是_________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高速公路某收费站出城方向有编号为![]() 的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
的五个小客车收费出口,假定各收费出口每20分钟通过小客车的数量分别都是不变的.同时开放其中的某两个收费出口,这两个出口20分钟一共通过的小客车数量记录如下:
收费出口编号 |
|
|
|
|
|
通过小客车数量(辆) | 260 | 330 | 300 | 360 | 240 |
在![]() 五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
五个收费出口中,每20分钟通过小客车数量最多的一个出口的编号是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,线段
,线段![]() ,
,![]() ,点
,点![]() 从点
从点![]() 开始绕着点
开始绕着点![]() 以
以![]() 的速度顺时针旋转一周回到点
的速度顺时针旋转一周回到点![]() 后停止,点
后停止,点![]() 同时出发沿射线
同时出发沿射线![]() 自
自![]() 点向
点向![]() 点运动,若点
点运动,若点![]() 、
、![]() 两点能恰好相遇,则点
两点能恰好相遇,则点![]() 运动的速度为________
运动的速度为________![]() ;
;

![]() 将一副三角板中的两块直角三角尺的直角顶点
将一副三角板中的两块直角三角尺的直角顶点![]() 按如图方式叠放在一起(其中,
按如图方式叠放在一起(其中,![]() ,
,![]() ,
,![]() ;
;![]() ).将三角尺
).将三角尺![]() 固定,另一三角尺
固定,另一三角尺![]() 的
的![]() 边从
边从![]() 边开始绕点
边开始绕点![]() 转动,转动速度与
转动,转动速度与![]() 问中
问中![]() 点速度相同,当
点速度相同,当![]() 且点
且点![]() 在直线
在直线![]() 的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 有可能的值及对应转动的时间;若不存在,请说明理由.
有可能的值及对应转动的时间;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)因式分解:(x2+4)2﹣16x2
(2)先化简,再求值:[(x+2y)2﹣(x+y)(x﹣y)﹣5y2]÷(2x),其中x=﹣2,y=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图像为直线
的图像为直线![]() .
.
(1)若直线![]() 与正比例函数
与正比例函数![]() 的图像平行,且过点(0,2),求直线
的图像平行,且过点(0,2),求直线![]() 的函数表达式;
的函数表达式;
(2)若直线![]() 过点(3,0),且与两坐标轴围成的三角形面积等于3,求
过点(3,0),且与两坐标轴围成的三角形面积等于3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为直径,
为直径,![]() 为弦.过
为弦.过![]() 延长线上一点
延长线上一点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售两种品牌的计算器,购买2个A品牌和3个B品牌的计算器共需280元;购买3个A品牌和1个B品牌的计算器共需210元.
(Ⅰ)求这两种品牌计算器的单价;
(Ⅱ)开学前,该商店对这两种计算器开展了促销活动,具体办法如下:A品牌计算器按原价的九折销售,B品牌计算器10个以上超出部分按原价的七折销售.设购买x个A品牌的计算器需要y1元,购买x个B品牌的计算器需要y2元,分别求出y1,y2关于x的函数关系式.
(Ⅲ)某校准备集体购买同一品牌的计算器,若购买计算器的数量超过15个,购买哪种品牌的计算器更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,BC交直径AD于点E,过点C作AD的垂线交AB的延长线于点G,垂足为F.连接OC.
(1)若∠G=48°,求∠ACB的度数;
(2)若AB=AE,求证:∠BAD=∠COF;
(3)在(2)的条件下,连接OB,设△AOB的面积为S1,△ACF的面积为S2.若tan∠CAF=![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com