
【题目】如图.矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD. 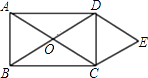
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为8 ![]() ,求AC的长.
,求AC的长.
【答案】
(1)证明:∵DE∥OC,CE∥OD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AO=OC=BO=OD.
∴四边形OCED是菱形
(2)解:∵∠ACB=30°,
∴∠DCO=90°﹣30°=60°.
又∵OD=OC,
∴△OCD是等边三角形.
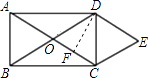
过D作DF⊥OC于F,则CF= ![]() OC,设CF=x,则OC=2x,AC=4x.
OC,设CF=x,则OC=2x,AC=4x.
在Rt△DFC中,tan60°= ![]() ,
,
∴DF= ![]() x.
x.
∴OCDF=8 ![]() .
.
∴x=2.
∴AC=4×2=8.
【解析】(1)熟记菱形的判定定理,本题可用一组邻边相等的平行四边形是菱形.(2)因为∠ACB=30°可证明菱形的一条对角线和边长相等,可证明和对角线构成等边三角形,然后作辅助线,根据菱形的面积已知可求解.
【考点精析】根据题目的已知条件,利用矩形的性质和解直角三角形的相关知识可以得到问题的答案,需要掌握矩形的四个角都是直角,矩形的对角线相等;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(﹣3,0),对称轴为x=﹣1.给出四个结论:①b2>4ac;②2a+b=0;③a﹣b+c=0;④5a<b.其中正确结论是( ) 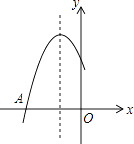
A.②④
B.①④
C.②③
D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆出租车从A地出发,在一条东西走向的街道上往返,每次行驶的情况(记向东为正)记录如下(x>5且x<14,单位:m):
行驶次数 | 第一次 | 第二次 | 第三次 | 第四次 |
行驶情况 | x | ﹣ | x﹣3 | 2(5﹣x) |
行驶方向(填“东”或“西”) |
|
|
|
|
(1)请将表格补充完整;
(2)求经过连续4次行驶后,这辆出租车所在的位置;
(3)若出租车行驶的总路程为41m,求第一次行驶的路程x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明参加某网店的“翻牌抽奖”活动,如图,4张牌分别对应价值5,10,15,20(单位:元)的4件奖品. 
(1)如果随机翻1张牌,那么抽中20元奖品的概率为 .
(2)如果随机翻2张牌,且第一次翻过的牌不再参加下次翻牌,请用列表或画树状图的方法求出所获奖品总值不低于30元的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过△ABC的三个顶点,与y轴相交于(0, ![]() ),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
),点A坐标为(﹣1,2),点B是点A关于y轴的对称点,点C在x轴的正半轴上.
(1)求该抛物线的函数关系表达式.
(2)点F为线段AC上一动点,过F作FE⊥x轴,FG⊥y轴,垂足分别为E、G,当四边形OEFG为正方形时,求出F点的坐标.
(3)将(2)中的正方形OEFG沿OC向右平移,记平移中的正方形OEFG为正方形DEFG,当点E和点C重合时停止运动,设平移的距离为t,正方形的边EF与AC交于点M,DG所在的直线与AC交于点N,连接DM,是否存在这样的t,使△DMN是等腰三角形?若存在,求t的值;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】鸡兔同笼问题是我国古代著名趣题之一,大约在 1500 年前,《孙子算经》中就记载了这个有趣的问题.书中是这样叙述的:“今有雉兔同笼,上有三十五头,下有九十四足,问雉兔各几何?”这四句话的意思是:有若干只鸡、兔同在一个笼子里,从上上面数,有 35 个头;从下面数,有 94 只脚 .求笼中各有几只鸡和兔?经计算可得( )

A. 鸡 20 只,兔 15 只 B. 鸡 12 只,兔 23 只
C. 鸡 15 只,兔 20 只 D. 鸡 23 只,兔 12 只
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级⑴班想买一些运动器材供班上同学阳光体育活动使用,班主任安排班长去商店买篮球和排球,下面是班长与售货员的对话:
班长:阿姨,您好! 售货员:同学,你好,想买点什么?

⑴根据这段对话,你能算出篮球和排球的单价各是多少吗?
⑵六一儿童节店里搞活动有两种套餐,1、套装打折:五个篮球和五个排球为一套装,套装打 八折:2、满减活动:999 减 100,1999 减 200;两种活动不重复参与,学校需要 15个篮球,13 个排球作为奖品,请问如何安排购买更划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个仓库共存有粮食60![]() .解决下列问题,3个小题都要写出必要的解题过程:
.解决下列问题,3个小题都要写出必要的解题过程:
(1)甲仓库运进粮食14![]() ,乙仓库运出粮食10
,乙仓库运出粮食10![]() 后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
后,两个仓库的粮食数量相等.甲、乙两个仓库原来各有多少粮食?
(2)如果甲仓库原有的粮食比乙仓库的2倍少3![]() ,则甲仓库运出多少
,则甲仓库运出多少![]() 粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
粮食给乙仓库,可使甲、乙两仓库粮食数量相等?
(3)甲乙两仓库同时运进粮食,甲仓库运进的数量比本仓库原存粮食数量的一半多1![]() ,乙仓库运进的数量是本仓库原有粮食数量加上8
,乙仓库运进的数量是本仓库原有粮食数量加上8![]() 所得的和的一半.求此时甲、乙两仓库共有粮食多少
所得的和的一半.求此时甲、乙两仓库共有粮食多少![]() ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com