
����Ŀ����ͼ��������y=ax2+bx+c������ABC���������㣬��y���ཻ�ڣ�0�� ![]() ������A����Ϊ����1��2������B�ǵ�A����y��ĶԳƵ㣬��C��x����������ϣ�
������A����Ϊ����1��2������B�ǵ�A����y��ĶԳƵ㣬��C��x����������ϣ�
��1����������ߵĺ�����ϵ����ʽ��
��2����FΪ�߶�AC��һ���㣬��F��FE��x�ᣬFG��y�ᣬ����ֱ�ΪE��G�����ı���OEFGΪ������ʱ�����F������꣮
��3������2���е�������OEFG��OC����ƽ�ƣ���ƽ���е�������OEFGΪ������DEFG������E�͵�C�غ�ʱֹͣ�˶�����ƽ�Ƶľ���Ϊt�������εı�EF��AC���ڵ�M��DG���ڵ�ֱ����AC���ڵ�N������DM���Ƿ����������t��ʹ��DMN�ǵ��������Σ������ڣ���t��ֵ������������˵�����ɣ�
���𰸡�
��1��
�⣺�ߵ�B�ǵ�A����y��ĶԳƵ㣬
�������ߵĶԳ���Ϊy�ᣬ
�������ߵĶ���Ϊ��0�� ![]() ����
����
�������ߵĽ���ʽ����Ϊy=ax2+ ![]() ��
��
��A����1��2����������y=ax2+ ![]() �ϣ�
�ϣ�
��a+ ![]() =2��
=2��
���a=�� ![]() ��
��
�������ߵĺ�����ϵ����ʽΪy=�� ![]() x2+
x2+ ![]()
��2��
�⣺�ٵ���F�ڵ�һ����ʱ����ͼ1��
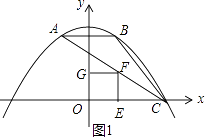
��y=0��� ![]() x2+
x2+ ![]() =0��
=0��
��ã�x1=3��x2=��3��
���C��������3��0����
��ֱ��AC�Ľ���ʽΪy=mx+n��
���� ![]() ��
��
��� 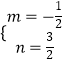 ��
��
��ֱ��AC�Ľ���ʽΪy=�� ![]() x+
x+ ![]() ��
��
��������OEFG�ı߳�Ϊp����F��p��p����
�ߵ�F��p��p����ֱ��y=�� ![]() x+
x+ ![]() �ϣ�
�ϣ�
�ੁ ![]() p+
p+ ![]() =p��
=p��
���p=1��
���F��������1��1����
�ڵ���F�ڵڶ�����ʱ��
ͬ���ɵã���F������Ϊ����3��3����
��ʱ��F�����߶�AC�ϣ�����ȥ��
������������F��������1��1��
��3��
�⣺����M��MH��DN��H����ͼ2��
��OD=t��OE=t+1��
�ߵ�E�͵�C�غ�ʱֹͣ�˶�����0��t��2��
��x=tʱ��y=�� ![]() t+
t+ ![]() ����N��t����
����N��t���� ![]() t+
t+ ![]() ����DN=��
����DN=�� ![]() t+
t+ ![]() ��
��
��x=t+1ʱ��y=�� ![]() ��t+1��+
��t+1��+ ![]() =��
=�� ![]() t+1����M��t+1����
t+1����M��t+1���� ![]() t+1����ME=��
t+1����ME=�� ![]() t+1��
t+1��
��Rt��DEM��DM2=12+���� ![]() t+1��2=
t+1��2= ![]() t2��t+2��
t2��t+2��
��Rt��NHM��MH=1��NH=���� ![]() t+
t+ ![]() ��������
�������� ![]() t+1��=
t+1��= ![]() ��
��
��MN2=12+�� ![]() ��2=
��2= ![]() ��
��
�� ��DN=DMʱ��
���� ![]() t+
t+ ![]() ��2=
��2= ![]() t2��t+2��
t2��t+2��
���t= ![]() ��
��
�ڵ�ND=NMʱ��
�� ![]() t+
t+ ![]() =
= ![]() =
= ![]() ��
��
���t=3�� ![]() ��
��
�۵�MN=MDʱ��
![]() =
= ![]() t2��t+2��
t2��t+2��
���t1=1��t2=3��
��0��t��2����t=1��
��������������DMN�ǵ���������ʱ��t��ֵΪ ![]() ��3��
��3�� ![]() ��1
��1
����������1���������ߵĶ���Ϊ��0�� ![]() ����Ȼ��ֻ�����ô���ϵ�������Ϳ���������ߵĺ�����ϵ����ʽ����2���ٵ���F�ڵ�һ����ʱ����ͼ1���������C�����ֱ꣬��AC�Ľ���ʽ����������OEFG�ı߳�Ϊp����F��p��p��������ֱ��AC�Ľ���ʽ���Ϳ������F�����ꣻ�ڵ���F�ڵڶ�����ʱ��ͬ���������F�����꣬��ʱ��F�����߶�AC�ϣ�����ȥ����3������M��MH��DN��H����ͼ2������ɵ�0��t��2��Ȼ��ֻ����t��ʽ�ӱ�ʾDN��DM2��MN2 �� �������������DN=DM����ND=NM����MN=MD�����۾Ϳɽ�����⣮
����Ȼ��ֻ�����ô���ϵ�������Ϳ���������ߵĺ�����ϵ����ʽ����2���ٵ���F�ڵ�һ����ʱ����ͼ1���������C�����ֱ꣬��AC�Ľ���ʽ����������OEFG�ı߳�Ϊp����F��p��p��������ֱ��AC�Ľ���ʽ���Ϳ������F�����ꣻ�ڵ���F�ڵڶ�����ʱ��ͬ���������F�����꣬��ʱ��F�����߶�AC�ϣ�����ȥ����3������M��MH��DN��H����ͼ2������ɵ�0��t��2��Ȼ��ֻ����t��ʽ�ӱ�ʾDN��DM2��MN2 �� �������������DN=DM����ND=NM����MN=MD�����۾Ϳɽ�����⣮
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮


 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������ʵ������У�ij���̶ӽ���һ���ˮ���Ĺ��̣���������y���죩��ÿ����ɵĹ�����x��m/�죩�ĺ�����ϵͼ����ͼ��ʾ����˫���ߵ�һ���֣� 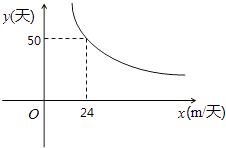
��1����������⣬��y��x֮��ĺ�������ʽ��
��2�����ù��̶���2̨�ھ����ÿ̨�ھ��ÿ���ܹ�����ˮ��15�ף��ʸù��̶����ö����������ɴ�������
��3�����Ϊ�˷�Ѵ�����Ľ�����Ҫ��������һ�����ڣ���30����㣩���������ôÿ������Ҫ��ɶ����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017��9��11�գ�������ɫ����������������Ϊ����������е��Ľ���̬����֪ʶ�������ʽ������ijУ��֯ȫУѧ�����������ʦ��ȡ�˰��ϵ�һ����8��ѧ���ijɼ�������80��Ϊ���������ķ�����������ʾ������ķ����ø�����ʾ���ɼ���¼���£���3��+7����12��+18��+6����5����21��+14
��1����߷ֱ���ͷֶ���ٷ֣���һ����ƽ��ÿ�˵ö��ٷ֣�
��2�����涨���ɼ�����80�ֵ�ѧ�����з�ÿ�˼�3�֣��ɼ���60��80�ֵ�ѧ�����з�ÿ�˼�2�֣��ɼ���60�����µ�ѧ�����з�ÿ�˿�1�֣���ô��һ�����ѧ�����Ӳ��зֶ��ٷ֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ����ཻ�ڵ�O��DE��AC��CE��BD�� 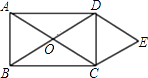
��1����֤���ı���OCED�����Σ�
��2������ACB=30�㣬����OCED�����Ϊ8 ![]() ����AC�ij���
����AC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ۿ�λ�ڶ�������ĺ������ϣ���Զ�����š������������ִ�ͬʱ�뿪�ۿڣ�������һ�̶������У���Զ������ÿСʱ����16�������������ÿСʱ����12��������뿪�ۿ�һ����Сʱ�����30������֪����Զ�������ض��������У���֪���������������ĸ������У�Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��ֱ��
��ֱ��![]() �ϵ�һ�㣬
�ϵ�һ�㣬![]() ������һ�����ߣ�
������һ�����ߣ�![]() ƽ��
ƽ��![]() ��
��![]() ƽ��
ƽ��![]() .
.
(1)ͼ��![]() �IJ���Ϊ ;
�IJ���Ϊ ;
(2)��![]() ����
����![]() �Ķ���;
�Ķ���;
(3)![]() ��
��![]() ����������������ϵ?
����������������ϵ?

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ�ڿ�ѧ��ij������Ʒ�̵꿪չ��������������Żݷ�����
����һ���������Ա��ʱ��ƹ��������8.5���Żݣ�ƹ�����Ĺ���5������5�������ϲ�������8.5���Żݣ�5�����±��밴��۹���
��������������Ա��ʱ��ȫ����Ʒ���ܰ����Żݣ�С����С����̸���������£�

��Ա��ֻ�ޱ���ʹ�ã�
��1������̵����۵�ƹ������ÿ���ı�ۣ�
��2�����ƹ����ÿ��10Ԫ��С���蹺��ƹ������6����ƹ����a�У���ش��������⣺
���������һ�뷽��������Ǯ��һ���࣬��a��ֵ��
��ֱ��д��һ��ǡ����aֵ��ʹ����һ�ȷ������Żݣ�
��ֱ��д��һ��ǡ����aֵ��ʹ�������ȷ���һ�Żݣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com