
【题目】如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为 ![]() 的中点.
的中点. 
(1)求证:AB=BC;
(2)求证:四边形BOCD是菱形.
【答案】
(1)证明:∵AB是⊙O的切线,
∴OB⊥AB,
∵∠A=30°,
∴∠AOB=60°,
∵OB=OC,
∴∠OCB=∠OBC= ![]() ∠AOB=30°,
∠AOB=30°,
∴∠A=∠OCB,
∴AB=BC
(2)证明:连接OD,
∵∠AOB=60°,
∴∠BOC=120°,
∵D为 ![]() 的中点,
的中点,
∴ ![]() =
= ![]() ,∠BOD=∠COD=60°,
,∠BOD=∠COD=60°,
∵OB=OD=OC,
∴△BOD与△COD是等边三角形,
∴OB=BD=OC=CD,
∴四边形BOCD是菱形.
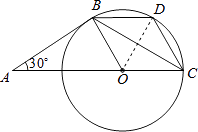
【解析】(1)由AB是⊙O的切线,∠A=30°,易求得∠OCB的度数,继而可得∠A=∠OCB=30°,又由等角对等边,证得AB=BC;(2)首先连接OD,易证得△BOD与△COD是等边三角形,可得OB=BD=OC=CD,即可证得四边形BOCD是菱形.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】某数学小组的10位同学站成一列做报数游戏,规则是:从前面第一位同学开始,每位同学依次报自己顺序数的倒数的2倍加1,第1位同学报( ![]() +1),第2位同学报(
+1),第2位同学报( ![]() +1),第3位同学报(
+1),第3位同学报( ![]() +1)…这样得到的n个数的积为 .
+1)…这样得到的n个数的积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别绘制成下列两个统计图:


根据以上信息,整理分析数据如下:
平均成绩(环) | 中位数(环) | 众数(环) | 方差 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)写出表格中a,b,c的值;
(2)分别运用表中的四个统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在第一象限,顶点
在第一象限,顶点![]() 、
、![]() 分别在函数
分别在函数![]() 图像的两个分支上,且
图像的两个分支上,且![]() 经过原点
经过原点![]() ,
,![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,已知
,已知![]() 平分四边形
平分四边形![]() 的面积.
的面积.
(1)证明:![]() :
:
(2)求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在李村河治理工程实验过程中,某工程队接受一项开挖水渠的工程,所需天数y(天)与每天完成的工程量x(m/天)的函数关系图象如图所示,是双曲线的一部分. 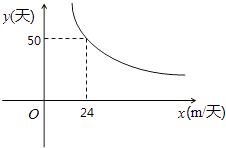
(1)请根据题意,求y与x之间的函数表达式;
(2)若该工程队有2台挖掘机,每台挖掘机每天能够开挖水渠15米,问该工程队需用多少天才能完成此项任务?
(3)如果为了防汛工作的紧急需要,必须在一个月内(按30天计算)完成任务,那么每天至少要完成多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个在平面直角坐标系中从原点开始的回形图,其中回形通道的宽和OA的长都是1.
(1)观察图形填写表格:
点 | 坐标 | 所在象限或坐标轴 |
A | ||
B | ||
C | ||
D | ||
E | ||
F |

(2)在图上将回形图继续画下去(至少再画出4个拐点);
(3)说出回形图中位于第一象限的拐点的横坐标与纵坐标之间的关系;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=mx2﹣5mx+1(m为常数,m>0),设该函数的图象与y轴交于点A,该图象上的一点B与点A关于该函数图象的对称轴对称.
(1)求点A,B的坐标;
(2)点O为坐标原点,点M为该函数图象的对称轴上一动点,求当M运动到何处时,△MAO的周长最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD. 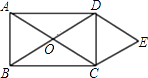
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的面积为8 ![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com