
【题目】如图,在平面直角坐标系中,已知点![]() 的坐标为
的坐标为![]() , 以
, 以![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴正半轴相交于点
轴正半轴相交于点![]() 过
过![]() 作
作![]() ,点
,点![]() 为弦
为弦![]() 上一点,连接
上一点,连接![]() .
.
(1)求![]() 的长度;
的长度;
(2)求证;直线![]() 是⊙
是⊙![]() 的切线;
的切线;
(3)若点![]() 是弧
是弧![]() 上一动点(
上一动点(![]() 点与
点与![]() 点不重合),过点
点不重合),过点![]() 的
的![]() 的切线
的切线![]() 交
交![]() 轴于
轴于![]() ,若
,若![]() 为直角三角形,试求出所有符合条件的点
为直角三角形,试求出所有符合条件的点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)见详解;(3)所有符合条件的点P的坐标是(-4,2),(4,2),(
;(2)见详解;(3)所有符合条件的点P的坐标是(-4,2),(4,2),(![]() ,4),(
,4),(![]() ,4).
,4).
【解析】
(1)根据勾股定理可以求得OB和OC的长度,从而可以得到B、C两点的坐标,即可得到答案;
(2)由![]() ,∠AOC=90°,则∠OAE=90°,由MA为半径,则AE是切线;
,∠AOC=90°,则∠OAE=90°,由MA为半径,则AE是切线;
(3)根据题意,画出相应的图形,然后利用分类讨论的方法可以得到点P的坐标.
解:(1)连接MB、MC,如图一所示,
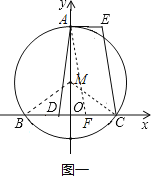
∵点M的坐标为(0,2),以M为圆心,以4为半径的圆与x轴相交于点B、C,
∴MB=MC=4,OM=2,
∵∠MOB=∠MOC=90°,
∴OB=![]() ,
,
∴OC=![]() ,
,
∴点B的坐标为(![]() ,0),点C的坐标为(
,0),点C的坐标为(![]() ,0),
,0),
∴![]() ;
;
(2)∵![]() ,∠AOC=90°,
,∠AOC=90°,
∴![]() ,
,
∵圆M与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,即MA为半径,
,即MA为半径,
∴AE是⊙M的切线;
(3)当△BP1G是直角三角形时,如图二所示,
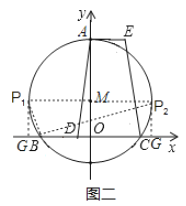
∵MA=MP1=4,点M的坐标为(0,2),
∴点P1的坐标为(-4,2);
当△BP2G是直角三角形时,如图二所示,
∵MA=MP2=4,点M的坐标为(0,2),
∴点P2的坐标为(4,2);
当△BP3G是直角三角形时,如图三所示,
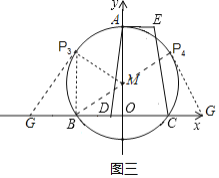
∵OB=![]() ,OM=2,
,OM=2,
∴tan∠MBO=![]() ,
,
∴∠MBO=30°,
∴∠MBP3=60°,
∵BM=MP3,
∴△BMP3是等边三角形,
∴BP3=4,
∴点P3的坐标为(![]() ,4);
,4);
当△BP4G是直角三角形时,如图三所示,
∵BP4=8,∠P4BG=30°时,
∴点P4的纵坐标是:8×sin30°=8×![]() =4,
=4,
横坐标是:![]() +8×cos30°=
+8×cos30°=![]() +8×
+8×![]() =
=![]() ,
,
∴点P4的坐标为(![]() ,4);
,4);
由上可得,若△BPG为直角三角形,所有符合条件的点P的坐标是(-4,2),(4,2),(![]() ,4),(
,4),(![]() ,4).
,4).


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() 为
为![]() 边中点,动点
边中点,动点![]() 从点
从点![]() 出发,沿着
出发,沿着![]() 的路径以每秒1个单位长度的速度运动到
的路径以每秒1个单位长度的速度运动到![]() 点,在此过程中线段
点,在此过程中线段![]() 的长度
的长度![]() 随着运动时间
随着运动时间![]() 的函数关系如图2所示,则
的函数关系如图2所示,则![]() 的长为( )
的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
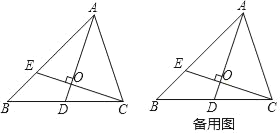
【题目】如图,△ABC中,D是边BC的中点,E是AB边上一点,且AD⊥CE于O,AD=AC=CE.
(1)求证:∠B=45°;
(2)求![]() 的值;
的值;
(3)直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90°,![]() ,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE =___________.
,点D、E分别在边AB上,且AD = 2,∠DCE = 45°,那么DE =___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE,PF分别交AB,AC于点E,F,给出以下五个结论:①△PFA≌△PEB,②EF=AP,③△PEF是等腰直角三角形,④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),S四边形AEPF=![]() S△ABC,上述结论中始终正确有 ( )
S△ABC,上述结论中始终正确有 ( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班50名学生参加“迎国庆,手工编织中国结”活动,要求每人编制4-7枚,活动结束后随机抽查了20名学生每人的编制量,并将统计数据绘制成扇形统计图(如图1)和条形统计图(如图2)(注:A代表4枚;B代表5枚;C代表6枚;D代表7枚)经确认扇形统计图是正确的,而条形统计图尚有一处是错误的.
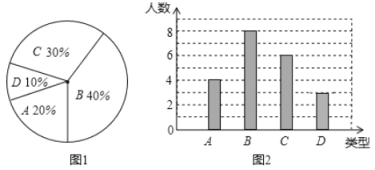
(1)条形统计图中存在的错误是:_______;
(2)写出这20名学生每人编制“中国结”数列的众数、中位数、平均数;
(3)估计这50名学生中编制“中国结”个数不少于6的人数;
(4)估计这50名学生中随机选取一名,求其编制“中国结”个数为6的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
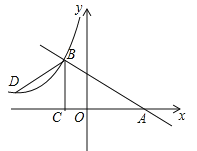
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)求该商店3月份这种商品的售价是多少元?
(2)如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com