
【题目】在平面直角坐标系中,点C沿着某条路径运动,以点C为旋转中心,将点A(0,4)逆时针旋转90°到点B(m,1),若﹣5≤m≤5,则点C运动的路径长为__.
【答案】![]()
【解析】
试题解析:如图1所示,在y轴上取点P(0,1),过P作直线l∥x轴,
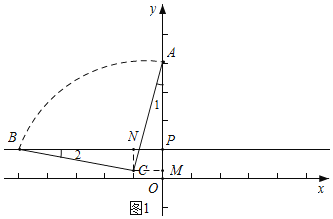
∵B(m,1),
∴B在直线l上,
∵C为旋转中心,旋转角为90°,
∴BC=AC,∠ACB=90°,
∵∠APB=90°,
∴∠1=∠2,
作CM⊥OA于M,作CN⊥l于N,则Rt△BCN≌Rt△ACM,
∴CN=CM,
若连接CP,则点C在∠BPO的平分线上,
∴动点C在直线CP上运动;
如图2所示,∵B(m,1)且-5≤m≤5,
∴分两种情况讨论C的路径端点坐标,

①当m=-5时,B(-5,1),PB=5,
作CM⊥y轴于M,作CN⊥l于N,
同理可得△BCN≌△ACM,
∴CM=CN,BN=AM,
可设PN=PM=CN=CM=a,
∵P(0,1),A(0,4),
∴AP=3,AM=BN=3+a,
∴PB=a+3+a=5,
∴a=1,
∴C(-1,0);
②当m=5时,B(5,1),如图2中的B1,此时的动点C是图2中的C1,
同理可得C1(4,5),
∴C的运动路径长就是CC1的长,
由勾股定理可得,CC1=![]() .
.


科目:初中数学 来源: 题型:
【题目】学生会要举办一个校园书画艺术展览会,为国庆献礼,小华和小刚准备将长AD为400cm,宽AB为130cm的矩形作品四周镶上彩色纸边装饰,如图所示,两人在设计时要求内外两个矩形相似,矩形作品面积是总面积的![]() ,他们一致认为上下彩色纸边要等宽,左右彩色纸边要等宽,这样效果最好,请你帮助他们设计彩色纸边宽度.
,他们一致认为上下彩色纸边要等宽,左右彩色纸边要等宽,这样效果最好,请你帮助他们设计彩色纸边宽度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出![]() 的x的取值范围;
的x的取值范围;
(3)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
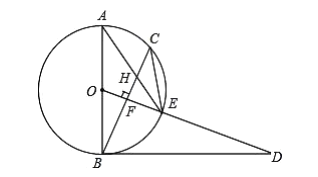
【题目】已知,如图,![]() 是⊙
是⊙![]() 的直径,点
的直径,点![]() 为⊙
为⊙![]() 上一点,
上一点,![]() 于点
于点![]() ,交⊙
,交⊙![]() 于点
于点![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 的延长线上一点,且
的延长线上一点,且![]() .
.
(1)试判断直线![]() 与⊙
与⊙![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若⊙![]() 的半径为
的半径为![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
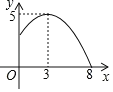
【题目】某小区有一半径为8m的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线.在距水池中心3m处达到最高,高度为5m,且各个方向喷出的水柱恰好在喷水池中心的装饰物处汇合.以水平方向为x轴,喷水池中心为原点建立如图所示的平面直角坐标系.
(1)求水柱所在抛物线对应的函数关系式;
(2)王师傅在喷水池维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8m的王师傅站立时必须在离水池中心多少米以内?
查看答案和解析>>
科目:初中数学 来源: 题型:
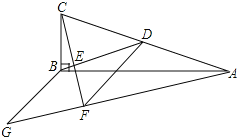
【题目】如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.
(1)求证:四边形BDFG为菱形;
(2)若AG=13,CF=6,求四边形BDFG的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以10元/千克的价格购进某种水果进行销售,经过市场调查获得部分数据如下表:
销售价格x(元/千克) | 10 | 13 | 16 | 19 | 22 |
日销售量y(千克) | 100 | 85 | 70 | 55 | 40 |
(1)请根据表中的数据,用所学过的一次函数、二次函数、反比例函数的知识刻画y与x之间的函数关系;
(2)该水果店应该如何确定这批水果的销售价格,才能使日销售利润最大?
(3)若该水果店平均每销售1千克这种水果会损耗a千克,当20≤x≤22时,水果店日获利的最大值为405元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中,边长为6,D、E分别是AB、AC的中点,连接DE,将△ADE绕点A顺时针旋转得到△AMN,其中D、E的对应点分别是M、N,直线BM与直线CN交于点F,若旋转360°,则点F经过的路径长是( )
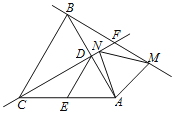
A.![]() B.8
B.8![]() C.
C.![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知OABC的顶点O与坐标原点重合,点A在x轴正半轴上,点B的坐标为(3,4),且B,C不在同一象限内,若反比例函数y=![]() 的图象经过线段AB的中点D,则四边形ODBC的面积为____.
的图象经过线段AB的中点D,则四边形ODBC的面积为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com