
【题目】已知等腰△ABC的顶角∠A=36°(如图). 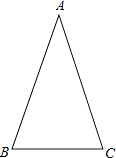
(1)作底角∠ABC的平分线BD,交AC于点D(用尺规作图,不写作法,但保留作图痕迹,然后用墨水笔加墨);
(2)通过计算说明△ABD和△BDC都是等腰三角形.
【答案】
(1)解:如图所示:
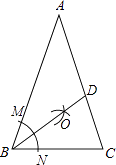
BD即为所求;
(2)解:∵∠A=36°,
∴∠ABC=∠C=(180°﹣36°)÷2=72°,
∵BD平分∠ABC,
∴∠ABD=∠DBC=72°÷2=36°,
∴∠CDB=180°﹣36°﹣72°=72°,
∵∠A=∠ABD=36°,∠C=∠CDB=72°,
∴AD=DB,BD=BC,
∴△ABD和△BDC都是等腰三角形.
【解析】(1)首先以B为圆心,任意长为半径画弧,两弧交AB、BC于M、N两点;再分别以M、N为圆心,大于 ![]() MN长为半径画弧,两弧交于一点O,画射线BO交AC于D.(2)根据三角形内角和为180°计算出∠ABC,∠C,∠CDB,∠ABD,∠DBC的度数,再根据等角对等边可证出结论.
MN长为半径画弧,两弧交于一点O,画射线BO交AC于D.(2)根据三角形内角和为180°计算出∠ABC,∠C,∠CDB,∠ABD,∠DBC的度数,再根据等角对等边可证出结论.


科目:初中数学 来源: 题型:
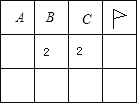
【题目】Windows2000下有一个有趣的游戏“扫雷”,下图是扫雷游戏的一部分:(说明:图中数字2表示在以该数字为中心的8个方格中有2个地雷).小旗表示该方格已被探明有地雷,现在还剩下A、B、C三个方格未被探明,其它地方为安全区(包括有数字的方格)
(1)现在还剩下几个地雷?
(2)A、B、C三个方格中有地雷的概率分别是多大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,直线y= ![]() x+6与x轴、y轴分别交于点A、C两点,点B的横坐标为2.
x+6与x轴、y轴分别交于点A、C两点,点B的横坐标为2. 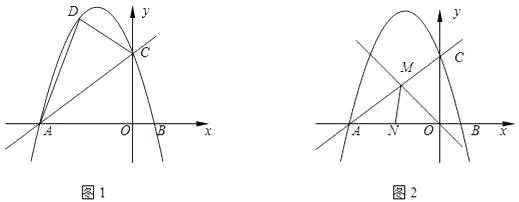
(1)求A、C两点的坐标和抛物线的函数关系式;
(2)点D是直线AC上方抛物线上任意一点,P为线段AC上一点,且S△PCD=2S△PAD , 求点P的坐标;
(3)如图2,另有一条直线y=﹣x与直线AC交于点M,N为线段OA上一点,∠AMN=∠AOM.点Q为x轴负半轴上一点,且点Q到直线MN和直线MO的距离相等,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB:BC=3:4,AC=5,点P从点A出发,以每秒1个单位的速度,沿△ABC边A→B→C→A的方向运动,运动时间为t秒.
(1)求AB与BC的长;
(2)在点P的运动过程中,是否存在这样的点P,使△CDP为等腰三角形?若存在,求出t值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,点C、D在线段AB上,D是线段AB的中点,AC=![]() AD ,CD=4 ,求线段AB的长.
AD ,CD=4 ,求线段AB的长.
![]()
(2)如图,点O是直线AB上的一点,OD是∠AOC的平分线,OE是∠COB的平分线,若∠AOD=14°,求∠DOE、∠BOE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一工地计划租用甲、乙两辆车清理淤泥,从运输量来估算:若租两辆车合运,10天可以完成任务;若单独租用乙车完成任务则比单独租用甲车完成任务多用15天.
(1)甲、乙两车单独完成任务分别需要多少天?
(2)已知两车合运共需租金65000元,甲车每天的租金比乙车每天的租金多1500元.试问:租甲乙车两车、单独租甲车、单独租乙车这三种方案中,哪一种租金最少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
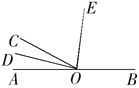
【题目】已知:如图所示,B、C、D三点在同一条直线上,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )

A. ∠A与∠D互为余角 B. ∠A=∠2 C. △ABC≌△ CED D. ∠1=∠2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com