练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    19．用配方法求：
    （1）代数式2x2-6x+1的最小值；
    （2）代数式-3x2+5x-1的最大值．

    分析 （1）先提取二次项系数，再配方，根据任何数的完全平方一定是非负数即可求解；
    （2）把原式根据配方法化成：-3x2+5x-1=-3（x-$\frac{5}{6}$）2+$\frac{13}{12}$即可得出最大值．

    解答 解：（1）2x2-6x+1
    =2（x2-3x+$\frac{9}{4}$）+1-$\frac{9}{2}$
    =2（x-$\frac{3}{2}$）2-$\frac{7}{2}$
    所以2x2-6x+1的最小值是-$\frac{7}{2}$．
    （2）-3x2+5x-1
    =-3（x2-$\frac{5}{3}$x+$\frac{25}{36}$）+$\frac{25}{12}$-1
    =-3（x-$\frac{5}{6}$）2+$\frac{13}{12}$
    所以-3x2+5x-1的最大值$\frac{13}{12}$．

    点评 此题考查了配方法的应用，解题时要注意配方法的步骤．注意在变形的过程中不要改变式子的值．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    9．如图，点A、B、C、D在⊙O上，∠A=60°，∠B=90°，AB=2，CD=1，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

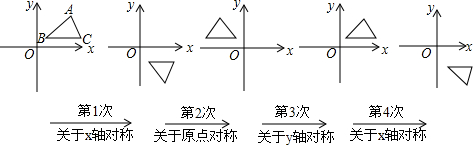
    10．如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（a，b），则经过第2014次变换后所得A点坐标是（　　）
    A．（a，-b）B．（-a，-b）C．（-a，b）D．（a，b）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

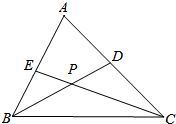    7．如图，在△ABC中，BD、CE分别是∠ABC，∠ACB的平分线．
    （1）若∠ABC=60°，∠ACB=40°时，求∠BPC的度数．
    （2）当∠A=80°时，求∠BPC的度数．
    （3）当∠A=x时，用含x代数式表示∠BPC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知分式$\frac{6a+18}{{a}^{2}-9}$的值为负整数，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．如图，在△ABC中，∠C=40°，∠B=80°，AD平分∠CAB，求：
    （1）∠1的度数；
    （2）求∠ADC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．画出函数y=-2x2的图象，并根据图象，求：
    （1）x=1，-1.2时y的值；
    （2）y=-2，-4时x的坐标（精确到0.1）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．Rt△ABC中，∠C=90°，AC=15，AB=25，则Rt△ABC的面积是150．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

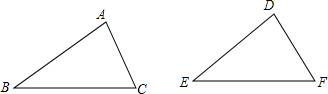    9．如图，下面的四组条件：
    ①∠B=∠E．∠C=∠F、AC=DF；
    ②AB=DE，∠B=∠E，BC=EF：
    ③∠B=∠E，BC=EF，∠C=∠F：
    ④AB=DE，AC=DF，∠B=∠E．
    其中，能使△ABC≌△DEF的条件共有①②③．

    查看答案和解析>>

    同步练习册答案