
分析 先把$\frac{6a+18}{{a}^{2}-9}$转化为$\frac{6(a+3)}{(a+3)(a-3)}=\frac{6}{a-3}$的形式,然后根据已知是负整数得出a-3=-1或a-3=-2或a-3=-3或a-3=-6,求出以后判断即可.
解答 解:因为$\frac{6a+18}{{a}^{2}-9}$=$\frac{6(a+3)}{(a+3)(a-3)}=\frac{6}{a-3}$,
又因为分式$\frac{6a+18}{{a}^{2}-9}$的值为负整数,
可得:a-3=-1或a-3=-2或a-3=-3或a-3=-6,
解得:a=2或a=1或a=0或a=-3(不合题意,舍去),
所以a的值是2或1或0.
点评 本题考查了分式的值,约分.注意分式的分母等于零时,分式无意义.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:选择题
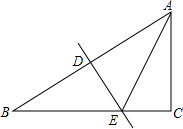 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=8,ED是边AB的垂直平分线,则△ACE的周长等于( )| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
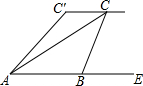 如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100m.当气球沿与BA平行的路线飘移10秒后到达C′处时,在A处测得气球的仰角为45°.求∠ACC′的度数.
如图,小敏、小亮从A,B两地观测空中C处一个气球,分别测得仰角为30°和60°,A,B两地相距100m.当气球沿与BA平行的路线飘移10秒后到达C′处时,在A处测得气球的仰角为45°.求∠ACC′的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com