
分析 首先根据概率的求法,求出第一题使用“求助”小明顺利通关的概率是多少,然后求出在第二题使用“求助”小明顺利通关的概率为多少;最后比较大小,判断出小明在第几题使用“求助”即可.
解答 解:第一题使用“求助”小明顺利通关的概率是:
$\frac{1}{2}×\frac{1}{4}=\frac{1}{8}$;
第二题使用“求助”小明顺利通关的概率是:
$\frac{1}{3}×\frac{1}{3}=\frac{1}{9}$;
∵$\frac{1}{8}>\frac{1}{9}$,
∴建议小明在第一题使用“求助”.
故答案为:一.
点评 此题主要考查了概率的意义和应用,要熟练掌握,解答此题的关键是分别求出第一题使用“求助”小明顺利通关的概率、第二题使用“求助”小明顺利通关的概率各是多少.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
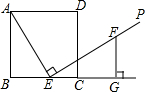 如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.
如图,E是正方形ABCD的边BC上的一个动点(E与B、C两点不重合),过点E作射线EP⊥AE,在射线EP上截取线段EF,使得EF=AE,过点F作FG⊥BC交BC的延长线于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 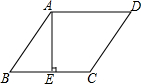 平行四边形ABCD中,AE⊥BC,则平行四边形ABCD的面积为:$\frac{1}{2}$BC×AE 平行四边形ABCD中,AE⊥BC,则平行四边形ABCD的面积为:$\frac{1}{2}$BC×AE | |
| B. | 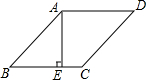 菱形ABCD中,AE⊥BC,则菱形ABCD的面积为:$\frac{1}{2}$BC×AE 菱形ABCD中,AE⊥BC,则菱形ABCD的面积为:$\frac{1}{2}$BC×AE | |
| C. | 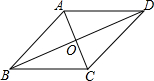 菱形ABCD中,对角线交于点O,则菱形ABCD的面积为:AC×BD 菱形ABCD中,对角线交于点O,则菱形ABCD的面积为:AC×BD | |
| D. | 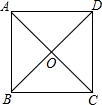 正方形ABCD中,对角线交于点O,则正方形ABCD的面积为:$\frac{1}{2}$AC×BD 正方形ABCD中,对角线交于点O,则正方形ABCD的面积为:$\frac{1}{2}$AC×BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
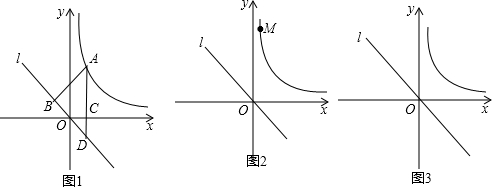
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
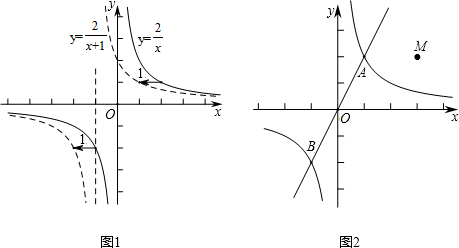
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com