
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 先确定两点确定一条直线;不同三点最多可确定3条直线;不同4点最多可确定(1+2+3)条直线,不同5点最多可确定(1+2+3+4)条直线,于是可根据此规律得到平面上不同的8个点最多可确定(1+2+3+4+5+6+7)=28条直线.
解答 解:两点确定一条直线;不同三点最多可确定3条直线;不同4点最多可确定(1+2+3)条直线,不同5点最多可确定(1+2+3+4)条直线,
因为1+2+3+4+5+6+7=28,
所以平面上不同的8个点最多可确定28条直线.
故选C.
点评 本题考查了直线、射线、线段:直线用一个小写字母表示,如:直线l,或用两个大写字母(直线上的)表示,如直线AB;射线是直线的一部分,用一个小写字母表示,如:射线l;用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边;线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA).


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为9m.
如图,小明用长为3m的竹竿CD做测量共计,测量学校旗杆AB的高度,移动竹竿,使O、C、A在同一直线上,此时OD=6m,DB=12m,则旗杆AB的高为9m.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3x+(10-x)=20 | B. | 4(x+0.5)+x=7 | C. | x=-$\frac{1}{2}$x+3 | D. | $\frac{1}{7}$(x+14)=$\frac{1}{4}$(x+20) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
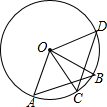 如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )
如图,在⊙O中,已知$\widehat{AB}$=$\widehat{CD}$,则AC与BD的关系是( )| A. | AC=BD | B. | AC<BD | C. | AC>BD | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
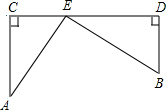 如图所示,在铁路线CD同侧有两个村庄A,B,它们到铁路线的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25,现在要在铁路旁建一个农副产品收购站E,使A,B两村庄到收购站的距离相等,用你学过的知识,通过计算,确定点E的位置.
如图所示,在铁路线CD同侧有两个村庄A,B,它们到铁路线的距离分别是15km和10km,作AC⊥CD,BD⊥CD,垂足分别为C,D,且CD=25,现在要在铁路旁建一个农副产品收购站E,使A,B两村庄到收购站的距离相等,用你学过的知识,通过计算,确定点E的位置.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com