练习册

  • 练习册
  • 试题
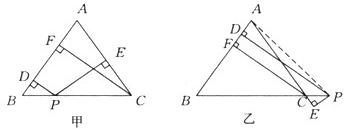
    精英家教网 > 初中数学 > 题目详情

    如图甲所示，若△ABC与△DCB是全等图形，且A与D，B与C是对应顶点，则进行以下变换可以使这两个三角形重合：

    先把△ABC沿着______，如图乙所示；

    再把△ABC绕着______，如图丙所示；

    最后把△ABC沿着______，如图丁所示．
    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图甲所示，在△ABC中，AB=AC，在底边BC上有任意一点P，则P点到两腰的距离之和等于定长（腰上的高），即PD+PE=CF，若P点在BC的延长线上，那么请你猜想PD、PE和CF之间存在怎样的等式关系？写出你的猜想并加以证明．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    某数学兴趣小组开展了一次活动，过程如下：
    设∠BAC=θ（0°＜θ＜90°）．现把小棒依次摆放在两射线之间，并使小棒两端分别落在射线AB，AC上．
    活动一：
    如图甲所示，从点A1开始，依次向右摆放小棒，使小棒与小棒在端点处互相垂直，A1A2为第1根小棒．
    数学思考：
    （1）小棒能无限摆下去吗？答：
     
    ．（填“能”或“不能”）
    （2）设AA1=A1A2=A2A3=1．
    ①θ=
     
    度；
    ②若记小棒A2n-1A2n的长度为an（n为正整数，如A1A2=a1，A3A4=a2，…） 求出此时a2，a3的值，并直接写出an（用含n的式子表示）．
    精英家教网

    活动二：
    如图乙所示，从点A1开始，用等长的小棒依次向右摆放，其中A1A2为第1根小棒，且A1A2=AA1．
    数学思考：
    （3）若已经摆放了3根小棒，θ1=
     
    ，θ2=
     
    ，θ3=
     
    ；（用含θ的式子表示）
    （4）若只能摆放4根小棒，求θ的范围．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•乐山模拟）如图甲，AB⊥BD，CD⊥BD，AP⊥PC，垂足分别为B、P、D，且三个垂足在同一直线上，我们把这样的图形叫“三垂图”．

    （1）证明：AB•CD=PB•PD．
    （2）如图乙，也是一个“三垂图”，上述结论成立吗？请说明理由．
    （3）已知抛物线与x轴交于点A（-1，0），B（3，0），与y轴交于点（0，-3），顶点为P，如图丙所示，若Q是抛物线上异于A、B、P的点，使得∠QAP=90°，求Q点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图甲所示，已知抛物线经过原点O和x轴上另一点E，顶点M的坐标为（2，4）；
    （1）求抛物线函数关系式；
    （2）矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3，将矩形ABCD以每秒1个单位长度的速度从图甲所示的位置沿x轴的正方向匀速平移，同时一动点P也以相同的速度从点A出发向B匀速移动，设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图乙所示）．
    ①当t=
    52
    时，判断点P是否在直线ME上，并说明理由；
    ②设以P、N、C、D为顶点的多边形面积为S，试问S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由；
    ③现将甲图中的抛物线向右平移m（m＞0）个单位，所得抛物线与x轴交于G、F两点，与原抛物线交于点Q，设△FGQ的面积为S，求S关于m的函关系式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    已知△ABC内接于⊙O，过点A作直线EF。

    (1）如图甲所示，若AB为⊙O的直径，要使EF成为⊙O的切线，还需要添加的一个条件是（至少说出两种）：（1）_______；（2）__________。

    　　　

    　　

    (2）如图乙所示，若AB不是⊙O的直径而是弦，且∠CAE =∠B，EF是⊙O的切线吗？试证明你的判断。

    查看答案和解析>>

    同步练习册答案