

分析 (1)由15<20,由总价=单价×数量建立式子求出其解即可;
(2)由条件可以得出东东家7月份的水费=第一级20吨的水费+第一级20吨的水费+超过40吨部分的水费,列出代数式化简即可;
(3)设其中一个月的用水量是x吨,则另一个月为(42-x)吨,分情况讨论:当0≤x≤20和x>20,由10月份的水费+11月份的水费=108.8元建立方程求出其解,进一步求解.
解答 解:(1)15×2.5=37.5(元).
故这个月的水费为37.5元.
(2)20×2.5+20×3.45+6.3(a-40)
=50+69+6.3a-252
=6.3a-133(元).
(3)设其中一个月的用水量是x吨,则另一个月为(42-x)吨.根据题意得:
①当0≤x≤20,则2.5x+50+3.45(42-x)=108.8,解得x=18.
故这两个月的用水量分别是18吨,24 吨;
②当两个月用水量都超过大于20小于40时,40×2.5+2×3.45=106.9(元),
106.9元<108.8元,不合题意.
点评 本题考查了代数式表示数的运用,列一元一次方程解实际问题的运用,分类讨论思想的运用,解答时根据总费用=各部分费用之和建立方程是关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{3}{5}$<-$\frac{4}{7}$ | B. | x-1是有理数,它的倒数是$\frac{1}{x-1}$ | ||
| C. | 若|a|=|b|,则a=b | D. | 若|a|=-a,则a<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
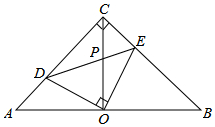 如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com