
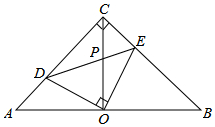
 如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )
如图,在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,点D、E分别在直角边AC、BC上,且∠DOE=90°,DE交OC于点P.则下列结论:①∠AOD=∠COE;②图形中全等的三角形有3对; ③△ABC的面积等于四边形CDOE的面积的2倍;④CD+CE=$\sqrt{2}$OA;⑤AD2+BE2=2OD2,其中正确的结论有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 由同角的锐角互余可判断①;结合等腰直角三角形的性质可证明△AOD≌△COE,可得到AD=CE,则可求得CD=BE,可证明△COD≌△BOE,且△AOC≌△BOC,可判断②和③;由全等三角形的性质可知CE=AD,BE=CD,则可得到CD+CE=BC,可判断④;同理可得到AD2+BE2=CE2+CD2=DE2=OD2+OE2可判断⑤;可求得答案.
解答 解:
∵在等腰直角△ACB中,∠ACB=90°,O是斜边AB的中点,
∴CO⊥AB,且AO=CO=BO,∠OCB=∠OAC=∠B=∠ACO=45°,
∴∠AOD+∠COD=∠COD+∠COE=90°,
∴∠AOD=∠COE,故①正确;
在△AOD和△COE中
$\left\{\begin{array}{l}{∠A=∠OCE}\\{AO=CO}\\{∠AOD=∠COE}\end{array}\right.$
∴△AOD≌△COE(ASA),
∴AD=CE,且AC=BC,
∴CD=BE,
在△COD和△BOE中
$\left\{\begin{array}{l}{CD=BE}\\{∠DCO=∠B}\\{CO=BO}\end{array}\right.$
∴△COD≌△BOE(SAS),
又由等腰直角三角形的性质可得△AOC≌△BOC,
∴全等的三角形有3对,故②正确;
∵△AOD≌△COE,
∴S四边形CDOE=S△COD+S△COE=S△AOD+S△COD=S△AOC=$\frac{1}{2}$S△ABC,
∴S△ABC=2S四边形CDOE,故③正确;
∵CD=BE,
∴CD+CE=CE+BE=BC,
∵CO=OB=OA,
∴BC=$\sqrt{2}$OA,
∴CD+CE=$\sqrt{2}$OA,故④正确;
∴AD2+BE2=CE2+CD2=DE2=OD2+OE2=2OD2,故⑤正确;
综上可知正确的有5个,
故选D.
点评 本题为三角形的综合应用,涉及等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识.利用等腰直角三角形的性质证明三角形全等是解题的关键,需要掌握全等三角形的判定方法.本题综合性较强,考查知识点较多,难度适中.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 160 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a5=a10 | B. | $\sqrt{a+b}$=$\sqrt{a}$+$\sqrt{b}$ | C. | $\sqrt{{a}^{2}}$=a | D. | (-a3)6=a18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com