练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

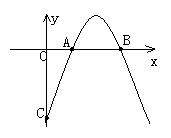
    如图,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0) , 且x1+x2=4, 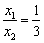.(1)求抛物线的代数表达式;

        (2)设抛物线与y轴交于C点,求直线BC的表达式;

        (3)求△ABC的面积.

     



    (1)解方程组, 得x1=1,x2=3

        故 ,解这个方程组,得b=4,c=-3.

        所以,该抛物线的代数表达式为y=-x2+4x-3.

        (2)设直线BC的表达式为y=kx+m.

        由(1)得,当x=0时,y=-3,故C点坐标为(0,-3).

        所以, 解得

        ∴直线BC的代数表达式为y=x-3

        (3)由于AB=3-1=2,OC=│-3│=3.

        故S△ABC=AB·OC=×2×3=3.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如果抛物线y＝a(x十)2+的对称轴是x＝－2，开口大小和方向与抛物线y＝x2的相同，且经过原点，那么a＝    ，b＝    ，c＝    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图2－109所示的抛物线的解析式是    (    )

            A．y＝x2－x＋2    B．y=－x2－x＋2

    C．y＝x2＋x＋2    D．y=－x2＋x＋2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    根据下列表格的对应值：

    x

    3.23

    3.24

    3.25

    3.26

    ax2＋bx＋c

    －0.06

    －0.02

    0.03

    0.09

        判断方程 ax2＋bx＋c=0(a≠0，a，b，c为常数)的一个解x的取值范围是  (    )

            A．3＜x＜3.23       B．3．23＜x＜3.24

            C．3.24＜x＜3.25     D．3.25＜x＜3.26

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴只有一个交    点，则这个交点的坐标是     .

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，∠C＝90°，AB＝3 cm，BC＝2 cm，以点A为圆心、2 cm为半径作圆，则点C和⊙A的位置关系是    (    )

           A．点C在⊙A上              B．点C在⊙A外

           C．点C在⊙A内              D．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ⊙O的半径为10cm, A是⊙O上一点, B是OA中点, C点和B点的距离等于5cm, 则C点和⊙O的位置关系是   [   ]

    A．C在⊙O内   B．C在⊙O上

    C．C在⊙O外   D．C在⊙O上或C在⊙O内

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    下列语句中不正确的有

    ①  平分  弦的直径垂直于弦   ②圆是轴对称图形，任何一条直径都是它的对称轴  ③长度相等的两条弧是等弧

    A.3个                  B.2个                 

    C.1个                  D.以上都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图3－71所示，AB是半圆O的直径，C是半圆上一点，D是的中点，DH⊥AB，H是垂足，AC分别交BD，DH于E，F，试说明DF＝EF．

    查看答案和解析>>

    同步练习册答案