
【题目】学完《全等三角形》知识后知道:满足“SSA”的两个三角形不一定全等,如图①,∠A与AB分别是△ABC与△ABD公共角与公共边,且AC=AD,但△ABC与△ABD不全等,但在特殊条件下“SSA”也可以确定两个三角形全等.如图②,∠MAB为锐角,AB=5,点B到射线AM的距离为3,点C在射线AM上,BC=x,当x的取值范围是__________时,△ABC的形状、大小是唯一确定。
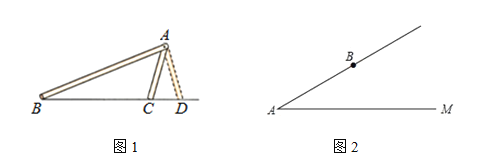
科目:初中数学 来源: 题型:
【题目】如图,已知:∠AOB=90°,OC平分∠AOB,点P在射线OC上.点E在射线OA上,点F在射线OB上,且∠EPF=90°.
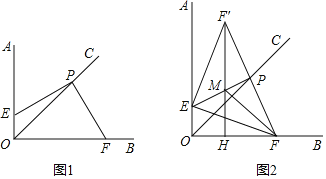
(1)如图1,求证:PE=PF;
(2)如图2,作点F关于直线EP的对称点F′,过F′点作FH⊥OF于H,连接EF′,F′H与EP交于点M.连接FM,图中与∠EFM相等的角共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在四边形 ![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求证:
,求证:![]() .
.

(2)如图,在离水面高度为 ![]() 米的岸上,有人用绳子拉船靠岸,开始时绳子
米的岸上,有人用绳子拉船靠岸,开始时绳子 ![]() 的长为
的长为 ![]() 米,此人以
米,此人以 ![]() 米每秒的速度收绳,
米每秒的速度收绳,![]() 秒后船移动到点
秒后船移动到点 ![]() 的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号).
的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
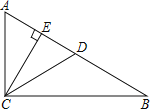
【题目】在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2![]() ,则AB=_____.
,则AB=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向东骑行2km到达A村,继续向东骑行3km到达B村,然后向西骑行9km到C村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用1个单位长度表示1km,请你在数轴上表示出A、B、C三个村庄的位置;
![]()
(2)C村离A村有多远?
(3)若摩托车每1km耗油0.03升,这趟路共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)学习《探索全等三角形条件》后,老师提出了如下问题:如图①,△ABC中,若AB=12,AC=8,求BC边上的中线AD的取值范围。同学通过合作交流,得到了如下的解决方法:延长AD到E,使DE=AD,连接BE.根据SAS可证得到△ADC≌△EDB,从而根据“三角形的三边关系”可求得AD的取值范围是 。解后反思:题目中出现“中点”“中线”等条件,可考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
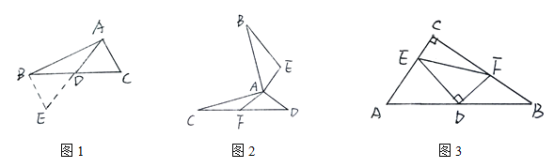
(直接运用)如图②,AB⊥AC,AD⊥AE,AB=AC,AD=AE,AF是ACD的边CD上中线.求证:BE=2AF.
(灵活运用)如图③,在△ABC中,∠C=90°,D为AB的中点,DE⊥DF,DE交AC于点E,DF交AB于点F,连接EF,试判断以线段AE、BF、EF为边的三角形形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
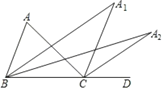
【题目】如图,∠ACD是△ABC的外角,∠ABC的平分线与∠ACD的平分线交于点A1,∠A1BC的平分线与∠A1CD的平分线交于点A2,∠A2BC的平分线与∠A2CD的平分线交于点A3.设∠A=64°.则(1)∠A1=________;(2)∠A3=_______。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用,因此学校随机抽取了部分同学就兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:

(1)学校这次调查共抽取了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,羽毛球部分所占的圆心角是 ;
(4)设该校共有学生1200名,请你估计该校有多少名学生喜欢跳绳?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com