
【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
【答案】(1)甲种办公桌每张400元,乙种办公桌每张600元;(2)当甲种办公桌购买30张,购买乙种办公桌10张时,y取得最小值,最小值为26000元.
【解析】(1)设甲种办公桌每张x元,乙种办公桌每张y元,根据“甲种桌子总钱数+乙种桌子总钱数+所有椅子的钱数=24000、10把甲种桌子钱数-5把乙种桌子钱数+多出5张桌子对应椅子的钱数=2000”列方程组求解可得;
(2)设甲种办公桌购买a张,则购买乙种办公桌(40-a)张,购买的总费用为y,根据“总费用=甲种桌子总钱数+乙种桌子总钱数+所有椅子的总钱数”得出函数解析式,再由“甲种办公桌数量不多于乙种办公桌数量的3倍”得出自变量a的取值范围,继而利用一次函数的性质求解可得.
(1)设甲种办公桌每张x元,乙种办公桌每张y元,
根据题意,得:
![]() ,
,
解得:![]() ,
,
答:甲种办公桌每张400元,乙种办公桌每张600元;
(2)设甲种办公桌购买a张,则购买乙种办公桌(40-a)张,购买的总费用为y,
则y=400a+600(40-a)+2×40×100
=-200a+32000,
∵a≤3(40-a),
∴a≤30,
∵-200<0,
∴y随a的增大而减小,
∴当a=30时,y取得最小值,最小值为26000元.


科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算):
价目表 | |
每月用水量 | 单价 |
不超过6 | 2元/ |
超出6 | 4元/ |
超出10 | 8元 |
请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5![]() ,则应交水费 元;3月份用水8
,则应交水费 元;3月份用水8![]() ,则应收水费 元;
,则应收水费 元;
(2)若该户居民4月份用水![]()
![]() (其中
(其中![]() ),则应交水费多少元(用含
),则应交水费多少元(用含![]() 的代数式表示,并化简);
的代数式表示,并化简);
(3)若该户居民5、6两个月共用水14![]() (6月份用水量超过了5月份),设5月份用水
(6月份用水量超过了5月份),设5月份用水![]()
![]() ,直接写出该户居民5、6两个月共交水费多少元(用含
,直接写出该户居民5、6两个月共交水费多少元(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
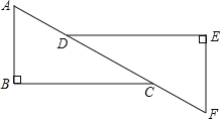
【题目】 如图,两块形状、大小完全相同的三角板按照如图所示的样子放置,找一找图中是否有互相平行的线段,完成下面证明:
证明:
∵∠______=∠______,
∴______∥______(______)(填推理的依据)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a,宽为2b的 长方形,沿图中虚线剪开分成四块小长方形,然后按如图2的形状拼成一个正方形。
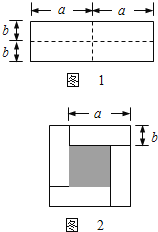
(1)图2的阴影部分的正方形的边长是 .
(2)用两种不同的方法求图中阴影部分的面积.
(方法1)S阴影= ;
(方法2)S阴影= ;
(3)观察如图2,写出(a+b)2、(a-b)2,ab三个代数式之间的等量关系.
(4)根据(3)题中的等量关系,解决问题:若x+y=10,xy=16,求x-y的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个角的差的绝对值等于![]() ,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如,
,就称这两个角互为反余角,其中一个角叫做另一个角的反余角,例如,![]() ,
,![]() ,
,![]() ,则
,则![]() 和
和![]() 互为反余角,其中
互为反余角,其中![]() 是
是![]() 的反余角,
的反余角,![]() 也是
也是![]() 的反余角.
的反余角.
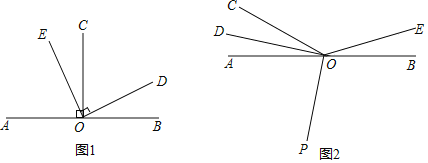
![]() 如图
如图![]() 为直线AB上一点,
为直线AB上一点,![]() 于点O,
于点O,![]() 于点O,则
于点O,则![]() 的反余角是______,
的反余角是______,![]() 的反余角是______;
的反余角是______;
![]() 若一个角的反余角等于它的补角的
若一个角的反余角等于它的补角的![]() ,求这个角.
,求这个角.
![]() 如图2,O为直线AB上一点,
如图2,O为直线AB上一点,![]() ,将
,将![]() 绕着点O以每秒
绕着点O以每秒![]() 角的速度逆时针旋转得
角的速度逆时针旋转得![]() ,同时射线OP从射线OA的位置出发绕点O以每秒
,同时射线OP从射线OA的位置出发绕点O以每秒![]() 角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时,
角的速度逆时针旋转,当射线OP与射线OB重合时旋转同时停止,若设旋转时间为t秒,求当t为何值时,![]() 与
与![]() 互为反余角
互为反余角![]() 图中所指的角均为小于平角的角
图中所指的角均为小于平角的角![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完《全等三角形》知识后知道:满足“SSA”的两个三角形不一定全等,如图①,∠A与AB分别是△ABC与△ABD公共角与公共边,且AC=AD,但△ABC与△ABD不全等,但在特殊条件下“SSA”也可以确定两个三角形全等.如图②,∠MAB为锐角,AB=5,点B到射线AM的距离为3,点C在射线AM上,BC=x,当x的取值范围是__________时,△ABC的形状、大小是唯一确定。
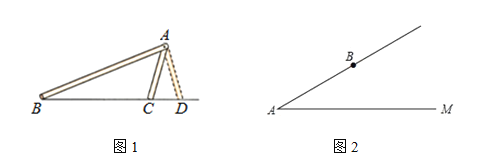
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,﹣2,+5,﹣6,+12,﹣9,+4,﹣14.(假定开始计时时,守门员正好在球门线上)
(1)守门员最后是否回到球门线上?
(2)守门员离开球门线的最远距离达多少米?
(3)如果守门员离开球门线的距离超过10米(不包括10米),则对方球员挑射极可能造成破门.请问在这一时间段内,对方球员有几次挑射破门的机会?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案,已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边(
表示直角三角形的两直角边(![]() ),下列四个说法:
),下列四个说法:

①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() .
.
其中说法正确的是 …………………………………………………………( )
A. ①② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
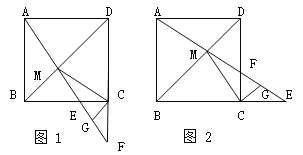
【题目】在边长为1的正方形ABCD中,点E是射线BC上一动点,AE与BD相交于点M,AE或其延长线与DC或其延长线相交于点F,G是EF的中点,连结CG.
(1)如图1,当点E在BC边上时.求证:①△ABM≌△CBM;②CG⊥CM.
(2)如图2,当点E在BC的延长线上时,(1)中的结论②是否成立?请写出结论,不用证明.
(3)试问当点E运动到什么位置时,△MCE是等腰三角形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com