
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算):
价目表 | |
每月用水量 | 单价 |
不超过6 | 2元/ |
超出6 | 4元/ |
超出10 | 8元 |
请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5![]() ,则应交水费 元;3月份用水8
,则应交水费 元;3月份用水8![]() ,则应收水费 元;
,则应收水费 元;
(2)若该户居民4月份用水![]()
![]() (其中
(其中![]() ),则应交水费多少元(用含
),则应交水费多少元(用含![]() 的代数式表示,并化简);
的代数式表示,并化简);
(3)若该户居民5、6两个月共用水14![]() (6月份用水量超过了5月份),设5月份用水
(6月份用水量超过了5月份),设5月份用水![]()
![]() ,直接写出该户居民5、6两个月共交水费多少元(用含
,直接写出该户居民5、6两个月共交水费多少元(用含![]() 的代数式表示).
的代数式表示).
【答案】(1)10,20;(2)应交水费(8a-52)元;(3)见解析.
【解析】
(1)根据题意,可以计算出该居民二月份和三月份的水费;
(2)根据题意,可以用a的代数式表示出4月份的水费;
(3)根据题意,利用分类讨论的方法可以解答本题.
解:(1)由表格可得,
若该户居民2月份用水5m3,则应交水费:2×5=10(元),
3月份用水8m3,则应收水费:2×6+4×(8-6)=12+4×2=12+8=20(元),
故答案为:10,20;
(2)由表格可得,
该户居民4月份用水am3(其中a>10m3),则应交水费:2×6+4×(10-6)+8(a-10)=(8a-52)元,
答:应交水费(8a-52)元;
(3)由题意可得,
x<14-x,得x<7,
当6<x<7,该户居民5、6两个月共交水费:[2×6+(x-6)×4]+[2×6+(14-x-6)×4]=32(元),
当4≤x≤6时,该户居民5、6两个月共交水费:2x+[2×6+(14-x)×4]=(-2x+68)(元),
当0≤x<4时,该户居民5、6两个月共交水费:2x+[2×6+(10-6)×4+(14-x)×8]=(140-6x)(元).


科目:初中数学 来源: 题型:
【题目】(1)已知等腰三角形的一边长等于8cm,一边长等于9cm,求它的周长;
(2)等腰三角形的一边长等于6cm,周长等于28cm,求其他两边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上有![]() 三点,分别表示有理数
三点,分别表示有理数![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒1个单位的速度向终点
出发,以每秒1个单位的速度向终点![]() 移动,当点
移动,当点![]() 运动到
运动到![]() 点时,点
点时,点![]() 从
从![]() 点出发,以每秒3个单位的速度向
点出发,以每秒3个单位的速度向![]() 点运动.
点运动.
(1)![]() 点出发3秒后所到的点表示的数为______,此时
点出发3秒后所到的点表示的数为______,此时![]() 两点的距离为_________.
两点的距离为_________.
(2)问当点![]() 从点
从点![]() 点出发几秒钟时,能追上点
点出发几秒钟时,能追上点![]() ?
?
(3)问当点![]() 从点
从点![]() 点出发几秒钟时,点
点出发几秒钟时,点![]() 和点
和点![]() 相距2个单位长度?直接写出此时点
相距2个单位长度?直接写出此时点![]() 在数轴上表示的有理数.
在数轴上表示的有理数.

查看答案和解析>>
科目:初中数学 来源: 题型:
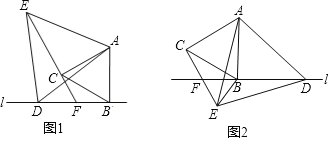
【题目】已知线段AB⊥直线l于点B,点D在直线l上,分别以AB,AD为边作等边三角形ABC和等边三角形ADE,直线CE交直线l于点F
(1)当点F在线段BD上时,如图1,线段DF,CE,CF之间的数量关系是 ;
(2)当点F在线段DB的延长线上时,如图2.
①(1)中的数量关系是否仍然成立?若成立,请写出证明过程;若不成立,请重新写出正确的结论,并写出证明过程;
②若等边△ABC和等边△ADE的边长分别是![]() 和
和![]() ,DF=3,求BE的长.
,DF=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.

(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)在直线l上找一点P,使PB′+PC的长最短;
(3)若△ACM是以AC为腰的等腰三角形,点M在小正方形的顶点上.这样的点M共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠AOB=90°,OC平分∠AOB,点P在射线OC上.点E在射线OA上,点F在射线OB上,且∠EPF=90°.
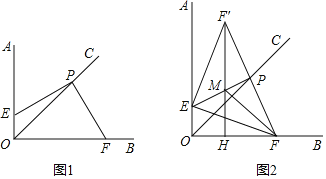
(1)如图1,求证:PE=PF;
(2)如图2,作点F关于直线EP的对称点F′,过F′点作FH⊥OF于H,连接EF′,F′H与EP交于点M.连接FM,图中与∠EFM相等的角共有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中:①PA=PB;②PO平分∠APB;③OA=OB④AB垂直平分OP,一定成立的是_________(填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(﹣1)×2=﹣2 | (﹣3)×(﹣4)×(﹣5)=﹣60 |
|
三个角上三个数的和 | 1+(﹣1)+2=2 | (﹣3)+(﹣4)+(﹣5)=﹣12 |
|
积与和的商 | (﹣2)÷2=﹣1 |
|
|
(2)请用你发现的规律求出图④中的数x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批甲、乙两种办公桌若干张,并且每买1张办公桌必须买2把椅子,椅子每把100元,若学校购进20张甲种办公桌和15张乙种办公桌共花费24000元;购买10张甲种办公桌比购买5张乙种办公桌多花费2000元.
(1)求甲、乙两种办公桌每张各多少元?
(2)若学校购买甲乙两种办公桌共40张,且甲种办公桌数量不多于乙种办公桌数量的3倍,请你给出一种费用最少的方案,并求出该方案所需费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com